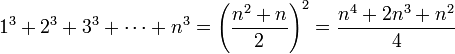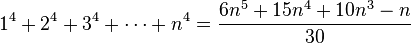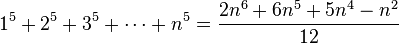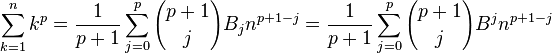Bernouli
கணிதத்தில் இந்த மரபு வழிக் கதை கூறப்படுவது உண்டு.நான் ஆய்லரை வைத்து கூறுகிறேன்.இது காஸ்[Gauss] மற்றும் ரமானுஜம் உட்பட பல அறிஞர்களின் வாழ்வில் நடந்ததாகவும் கூறுவர். ஆய்லர்(?) சிறுவனாக தொடக்கப் பள்ளியில் படித்துக் கொண்டிருந்த போது ஆசிரியர் மாணவர்களை ஒன்றில் இருந்து 100 வரை அனைவரும் கூட்டும் படி சொல்லிவிட்டு அவருக்கு இருந்த பணியை செய்யத் தொடங்கினார் .ஆசிரியரின் எண்ணம் எல்லோரும் மெதுவாகவே செயலை செய்வார்கள் அதற்குள் தன் பணியை முடிப்பதே அவர் எண்ணம்.ஆனால் ஆய்லர் உடனே 5050 என்ற சரியான விடையை கூறினாராம்.எப்படி சீக்கிரம் கண்டு பிடித்தாய் என்றதற்கு அவர் முறையை இவ்வாறு விளக்கினாராம்!!!.
மொத்தக் கூட்டுத் தொகை S
S= 1+2+ 3+……98+99.+100 (1)
திருப்பி எழுதினால் இப்படி வரும்
S=100+99+98+…3+2+1 (2)
(1)+(2)=2S=101+101+101+…+101+101=100X101
S=(100X101)/2=5050
அதாவது இது ஒரு கூட்டுத் தொடர் இதனை நேராகவும்,எதிராகவும் எழுதி கூட்டினால் ஒரே எண் வருகிறது.ஆகவே இந்த ஃபார்முலா இப்படிக் கூறலாம்
சரி இதுவும் படித்து இருப்போம்.இதற்கான நிரூபணம் கூட கொடுக்கலாம் எனினும் இப்பதிவில் இப்படியே எந்த அடுக்கு தொடருக்கும் கூட்டுத் தொகை காணும் முறை பற்றியே கூறுகிறோம். பயன்பாடுகள் நிரூபணத்தை விட எளிமையானது இயல்பானது.

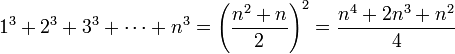
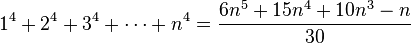
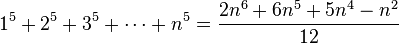

இப்பதிவில் இந்த பொதுவான் அடுக்குத் தொடரின் கூட்டுத் தொகைக்கு விடை காணும் முறை கற்கிறோம்.
S(n)=1^p+2^p+3^p….+n^p=?
இதுதான் ஃபார்முலா.
என்ன குழப்ப ஆரம்பித்து விட்டீர்களா என்கிறீர்களா? சரி கொஞ்சம் விளக்குவோம்!.
இந்த ஃபார்முலாவில்[தமிழ் பதம் என்ன?] நமக்கு தெரியாத இரு விஷயங்கள் உள்ளன
1 nCr
2 பெர்னொலி எண்கள்(Bj)
1)nCr
இந்த நிகழ்தகவு(probability) படித்தவர்களுக்கு nCr என்பதன் ஃபார்முலா தெரியும்.தொடர் பெருக்கல் [Factorial] என்பதை முதலில் தெரிந்து கொள்வோம்.
1*2*3*…..n=n!
5!=5*4*3*2*1=120
கணித மொழியில் இவ்வாறு குறிப்பிடுவார்கள்.
nCr என்பது பல பயன்பாடுகள் உடையது.இது தொடர் பெருக்கலை அடிப்படையாக கொண்ட ஃபார்முலா
nCr=
எ.கா 4C2=(4*3)/(2*1)=6. இதன் பயன்பாடுகள் மிக அதிகம்.
2)Bernouli numbers
B(k)
என்பது பெர்னொலி எண்கள் என அழைக்கப்படுகிறது.பெர்னொலி சுவிர்சர்லாந்தை சேர்ந்த கணித& அறிவியல் வல்லுனர்.பெர்னோலி எண்கள் கணக்கிட தெரிந்தால் எந்த அடுக்குத் தொடருக்கும் கூட்டுத் தொகை எளிதில் காண இயலும்.இத்தொடர்பை பயன்படுத்தி பெர்னொலி எண்கள் தொடர்ச்சியாக கணக்கிட இயலும்.

அதாவது எளிதாக கூறினால்
Bm= -1/(m+1))*[(m+1)
C0*
B0+(m+1)
C1*
B1+(m+1)
C2)*
B2+((m+1)
C3*
B3+....
+((m+1)
C(m+1)*
B(m-1)]
B0=1
B1=-1/2
B2= (-1/3)*[(3C0)*B0+(3C1)*B1]=-[B0+3B1]/3=-1/6
B3=B5=B7=.B(odd number)=0
B4= (-1/5)*[(5C0)*B0+(5C1)*B1+)*[(5C2)*B2+(5C3)*B3]
= (-1/5) *[1-5*(-1/2)+10*(1/6)=-(1/30)
| B0 | B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 |
B0 | 1(1) |
|
|
|
|
|
|
|
|
|
|
B1 | 1(1) | 2(-1/2) |
|
|
|
|
|
|
|
|
|
B2 | 1(1) | 3(-1/2) | 3(1/6) |
|
|
|
|
|
|
|
|
B3 | 1(1) | 4(-1/2) | 6(1/6) | 4(0) |
|
|
|
|
|
|
|
B4 | 1(1) | 5(-1/2) | 10(1/6) | 10(0) | 5(-1/30) |
|
|
|
|
|
|
B5 | 1(1) | 6(-1/2) | 15(1/6) | 20(0) | 15(-1/30) | 6(0) |
|
|
|
|
|
B6 | 1(1) | 7(-1/2) | 21(1/6) | 35(0) | 35(-1/30) | 21(0) | 7(1/42) |
|
|
|
|
B7 | 1(1) | 8(-1/2) | 28(1/6) | 56(0) | 70(-1/30) | 56(0) | 28(1/42 | 8(0) |
|
|
|
B8 | 1(1) | 9(-1/2) | 36(1/6) | 84(0) | 126(-1/30) | 126(0) | 84(1/42 | 36(0) | 9(−1/30) |
|
|
B9 | 1(1) | 10(-1/2) | 45(1/6) | 120(0) | 210(-1/30) | 252(0) | 210(1/42) | 120(0) | 45(−1/30) | 10(0) |
|
B10 | 1(1) | 11(-1/2) | 55(1/6) | 165(0) | 330(-1/30) | 462(0) | 462(1/42) | 330(0) | 165(−1/30) | 55(0) | 11(5/66) |
அடைப்புக்குறிக்குள் உள்ளது பெர்னொலி எண்கள்.வெளியில் உள்ளது nCr.பெர்னொலி எண்கள் கணக்கிடும் முறை புரிந்திருக்கும் என எண்ணுகிறேன். கணக்கிட்டு சரி பார்க்கவும்.
இப்போது அடுக்குத் தொடரின் கூட்டுத் தொகைக்கு ஒரே ஒரு எடுத்துக்காட்டு மட்டும் பார்த்து விடலாம்
p=10
S=1/(11)*[11C0*B0*n^11+11C1*B1*n^10+11C2*B2*n^9+11C4*B4*n^7+11C6*B6*n^5+11C8*B8*n^3+11C10*B0*n]
B3=B5=B7=B9=0
அட்டவணையில் இருந்து மதிப்புகளை(இறுதி வரிசை) இட்டால் ஃபார்முலா தயார்.
S10= (1/11)*[n^11-(11/2)*n^10+(55/6)*n^9-11n^7+(11)*n^5-(11/2)*n^3+(5/6)n]
இது போல் எந்தளவு அடுக்குத் தொடர்களின் கூடுதல் காண இயலும்.
சுருக்கமாக் அனைத்தையும் சொல்லி விடுகிறேன்.
1. nCr என்பதை அறிந்து கொள்ளவும்
2. பெர்னொலி எண்கள் தொடர்ச்சியாக் காணும் முறை அறிய வேண்டும்.
3.எந்த அடுக்குகளின் கூட்டுத் தொகை தேவையோ அதற்கேற்ற படி ஃபார்முலாவை விரிவுபடுத்தி மதிப்புகளை இட்டால் போதும்.சில முறை செய்து பார்த்தால் எளிதில் பிடி பட்டு விடும் நன்றி!!!!!!!!!!!!!!!!