சமரசம் உலாவும் இடமே!!!!: அடுக்குத் தொடர்களின்[integer power series] கூடுதல் காண்பது எப்படி?

Friday, November 4, 2011

அடுக்குத் தொடர்களின்[integer power series] கூடுதல் காண்பது எப்படி?

Bernouli

கணிதத்தில் இந்த மரபு வழிக் கதை கூறப்படுவது உண்டு.நான் ஆய்லரை வைத்து கூறுகிறேன்.இது காஸ்[Gauss] மற்றும் ரமானுஜம் உட்பட பல அறிஞர்களின் வாழ்வில் நடந்ததாகவும் கூறுவர். ஆய்லர்(?) சிறுவனாக தொடக்கப் பள்ளியில் படித்துக் கொண்டிருந்த போது ஆசிரியர் மாணவர்களை ஒன்றில் இருந்து 100 வரை அனைவரும் கூட்டும் படி சொல்லிவிட்டு அவருக்கு இருந்த பணியை செய்யத் தொடங்கினார் .ஆசிரியரின் எண்ணம் எல்லோரும் மெதுவாகவே செயலை செய்வார்கள் அதற்குள் தன் பணியை முடிப்பதே அவர் எண்ணம்.ஆனால் ஆய்லர் உடனே 5050 என்ற சரியான விடையை கூறினாராம்.எப்படி சீக்கிரம் கண்டு பிடித்தாய் என்றதற்கு அவர் முறையை இவ்வாறு விளக்கினாராம்!!!.

மொத்தக் கூட்டுத் தொகை S

S= 1+2+ 3+……98+99.+100 (1)

திருப்பி எழுதினால் இப்படி வரும்

S=100+99+98+…3+2+1 (2)

(1)+(2)=2S=101+101+101+…+101+101=100X101

S=(100X101)/2=5050

அதாவது இது ஒரு கூட்டுத் தொடர் இதனை நேராகவும்,எதிராகவும் எழுதி கூட்டினால் ஒரே எண் வருகிறது.ஆகவே இந்த ஃபார்முலா இப்படிக் கூறலாம்

$1 + 2 + 3 + \cdots + n = {n(n+1) \over 2} = {n^2 + n \over 2}$

சரி இதுவும் படித்து இருப்போம்.இதற்கான நிரூபணம் கூட கொடுக்கலாம் எனினும் இப்பதிவில் இப்படியே எந்த அடுக்கு தொடருக்கும் கூட்டுத் தொகை காணும் முறை பற்றியே கூறுகிறோம். பயன்பாடுகள் நிரூபணத்தை விட எளிமையான‌து இயல்பானது.

$1^2 + 2^2 + 3^2 + \cdots + n^2 = {n(n+1)(2n+1) \over 6} = {2n^3 + 3n^2 + n \over 6}$

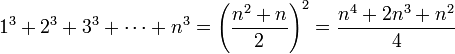
$1^3 + 2^3 + 3^3 + \cdots + n^3 = \left({n^2 + n \over 2}\right)^2 = {n^4 + 2n^3 + n^2 \over 4}$

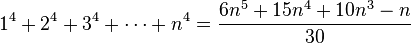
$1^4 + 2^4 + 3^4 + \cdots + n^4 = {6n^5 + 15n^4 + 10n^3 - n \over 30}$

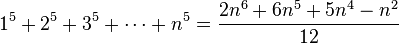
$1^5 + 2^5 + 3^5 + \cdots + n^5 = {2n^6 + 6n^5 + 5n^4 - n^2 \over 12}$

$1^6 + 2^6 + 3^6 + \cdots + n^6 = {6n^7 + 21n^6 + 21n^5 -7n^3 + n \over 42}$

இப்பதிவில் இந்த பொதுவான் அடுக்குத் தொடரின் கூட்டுத் தொகைக்கு விடை காணும் முறை கற்கிறோம்.

S(n)=1^p+2^p+3^p….+n^p=?

இதுதான் ஃபார்முலா.

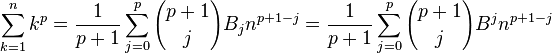
$\sum_{k=1}^n k^p = {1 \over p+1} \sum_{j=0}^p {p+1 \choose j} B_j n^{p+1-j} = {1 \over p+1} \sum_{j=0}^p {p+1 \choose j} B^j n^{p+1-j}$

என்ன குழப்ப ஆரம்பித்து விட்டீர்களா என்கிறீர்களா? சரி கொஞ்சம் விளக்குவோம்!.

இந்த ஃபார்முலாவில்[தமிழ் பதம் என்ன?] நமக்கு தெரியாத இரு விஷயங்கள் உள்ளன‌
1 nCr
2 பெர்னொலி எண்கள்(Bj)

1)nCr

இந்த நிகழ்தகவு(probability) படித்தவர்களுக்கு nCr என்பதன் ஃபார்முலா தெரியும்.தொடர் பெருக்கல் [Factorial] என்பதை முதலில் தெரிந்து கொள்வோம்.

1*2*3*…..n=n!

5!=5*4*3*2*1=120

கணித மொழியில் இவ்வாறு குறிப்பிடுவார்கள்.

$n!=\prod_{k=1}^n k \!$

$n! = \begin{cases} 1 & \text{if } n = 0, \\ (n-1)!\times n & \text{if } n > 0. \end{cases}$

nCr என்பது பல பயன்பாடுகள் உடையது.இது தொடர் பெருக்கலை அடிப்படையாக கொண்ட ஃபார்முலா

nCr=

$\binom nk=\frac{n^{\underline k}}{k!}=\frac{n!}{(n-k)!k!}=\frac{n^{\underline{n-k}}}{(n-k)!}=\binom n{n-k}.$

எ.கா 4C2=(4*3)/(2*1)=6. இதன் பயன்பாடுகள் மிக அதிகம்.

2)Bernouli numbers

B(k) என்பது பெர்னொலி எண்கள் என அழைக்கப்படுகிறது.பெர்னொலி சுவிர்சர்லாந்தை சேர்ந்த கணித& அறிவியல் வல்லுனர்.பெர்னோலி எண்கள் கணக்கிட தெரிந்தால் எந்த அடுக்குத் தொடருக்கும் கூட்டுத் தொகை எளிதில் காண இயலும்.இத்தொடர்பை பயன்படுத்தி பெர்னொலி எண்கள் தொடர்ச்சியாக கணக்கிட இயலும்.

அதாவது எளிதாக கூறினால்

Bm= -1/(m+1))*[(m+1)C0*B0+(m+1)C1*B1+(m+1)C2)*B2+((m+1)C3*B3+....
+((m+1)C(m+1)*B(m-1)]

B0=1

B1=-1/2

B2= (-1/3)*[(3C0)*B0+(3C1)*B1]=-[B0+3B1]/3=-1/6

B3=B5=B7=.B(odd number)=0

B4= (-1/5)*[(5C0)*B0+(5C1)*B1+)*[(5C2)*B2+(5C3)*B3]

= (-1/5) *[1-5*(-1/2)+10*(1/6)=-(1/30)

	B0	B1	B2	B3	B4	B5	B6	B7	B8	B9	B10
B0	1(1)
B1	1(1)	2(-1/2)
B2	1(1)	3(-1/2)	3(1/6)
B3	1(1)	4(-1/2)	6(1/6)	4(0)
B4	1(1)	5(-1/2)	10(1/6)	10(0)	5(-1/30)
B5	1(1)	6(-1/2)	15(1/6)	20(0)	15(-1/30)	6(0)
B6	1(1)	7(-1/2)	21(1/6)	35(0)	35(-1/30)	21(0)	7(1/42)
B7	1(1)	8(-1/2)	28(1/6)	56(0)	70(-1/30)	56(0)	28(1/42	8(0)
B8	1(1)	9(-1/2)	36(1/6)	84(0)	126(-1/30)	126(0)	84(1/42	36(0)	9(−1/30)
B9	1(1)	10(-1/2)	45(1/6)	120(0)	210(-1/30)	252(0)	210(1/42)	120(0)	45(−1/30)	10(0)
B10	1(1)	11(-1/2)	55(1/6)	165(0)	330(-1/30)	462(0)	462(1/42)	330(0)	165(−1/30)	55(0)	11(5/66)

அடைப்புக்குறிக்குள் உள்ளது பெர்னொலி எண்கள்.வெளியில் உள்ளது nCr.பெர்னொலி எண்கள் கணக்கிடும் முறை புரிந்திருக்கும் என எண்ணுகிறேன். கணக்கிட்டு சரி பார்க்கவும்.

இப்போது அடுக்குத் தொடரின் கூட்டுத் தொகைக்கு ஒரே ஒரு எடுத்துக்காட்டு மட்டும் பார்த்து விடலாம்

p=10

S=1/(11)*[11C0*B0*n^11+11C1*B1*n^10+11C2*B2*n^9+11C4*B4*n^7+11C6*B6*n^5+11C8*B8*n^3+11C10*B0*n]

B3=B5=B7=B9=0

அட்டவணையில் இருந்து மதிப்புகளை(இறுதி வரிசை) இட்டால் ஃபார்முலா தயார்.

S10= (1/11)*[n^11-(11/2)*n^10+(55/6)*n^9-11n^7+(11)*n^5-(11/2)*n^3+(5/6)n]

இது போல் எந்தளவு அடுக்குத் தொடர்களின் கூடுதல் காண இயலும்.

சுருக்கமாக் அனைத்தையும் சொல்லி விடுகிறேன்.

1. nCr என்பதை அறிந்து கொள்ளவும்

2. பெர்னொலி எண்கள் தொடர்ச்சியாக் காணும் முறை அறிய வேண்டும்.

3.எந்த அடுக்குகளின் கூட்டுத் தொகை தேவையோ அதற்கேற்ற படி ஃபார்முலாவை விரிவுபடுத்தி மதிப்புகளை இட்டால் போதும்.சில முறை செய்து பார்த்தால் எளிதில் பிடி பட்டு விடும் நன்றி!!!!!!!!!!!!!!!!

http://en.wikipedia.org/wiki/Bernoulli_number

http://en.wikipedia.org/wiki/Faulhaber%27s_formula

16 comments:

ஜோதிஜிNovember 5, 2011 at 5:13 AM
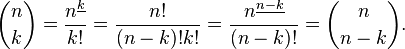
உங்க மண்டை முழுக்க மூளையாகவே இருக்குமோ? எல்லா ஆழமான விசயகளிலும் கலந்து அடிக்கீறீங்க.
ReplyDelete
Replies
சார்வாகன்November 5, 2011 at 6:43 AM
வாங்க நண்பர் ஜோதிஜி,
நலமா?.
கஷ்டப் பட்டு கண்டுபிடித்தவர்கள் (கணிணி இல்லாக் கால்த்திலேயே)பெர்னொலி,ஆய்லர் ,நியூட்டன்.....அதனை கொஞ்சம் எளிமைப் படுத்தி தமிழில் சொல்வது மட்டுமே நம் பணி.இதற்கு கொஞ்சம் உழைப்பு மட்டுமே தேவை!.அவ்வளவுதான்.சொல்லிய விடயமே முக்கியம்.சொல்லியவன் ஒரு கருவியே!!!!!!!!!.நான் இல்லையெனில் இன்னொருவர் சொல்வார் அவ்வளவுதான்.தமிழ் படுத்துவதற்குத்தான் சிரம‌மாக உள்ளது.யாரேனும் ஒத்துழைத்தால் நலமாக இருக்கும்.
நன்றி
ReplyDelete
Replies
K.s.s.RajhNovember 5, 2011 at 9:14 AM
அண்ணே படிக்கும் காலத்திலேயே எனக்கு கணிதம் என்றால் அலர்ஜ்சி.............நான் அடுத்த பதிவுக்கு வாரன்........ஹி.ஹி.ஹி.ஹி...........
ReplyDelete
Replies
சார்வாகன்November 5, 2011 at 9:22 AM
சரி நண்பர் ராஜ் ஒவ்வொருவருக்கும் ஒன்றில் ஈடுபாடு&திறமை.வருகைக்கும் கருத்து பதிவிற்கும் நன்றி!
ReplyDelete
Replies
narenNovember 5, 2011 at 4:31 PM
பதிவிற்கு நன்றி நண்பரே,
சித்திரமும் கைப்பழக்கம், செந்தமிழும் நாப்பழக்கம், கணிதமும் கிறுக்கல்(solving) பழக்கம்.
கணிதத்தை concept புரிந்து கிறுக்கிக் கொண்டிருந்தால் தானாக வந்துவிடும்.
பதிவு நல்ல விஷயத்தை சொன்னது. தமிழாக்கம் தொடரட்டும்.
ReplyDelete
Replies
சீனிவாசன்November 5, 2011 at 5:41 PM
சிறப்பான இடுகை நண்பரே, ஆர்வமுள்ளவர்களுக்கு நல்ல பயனளிக்கும் என நினைக்கிறேன். நம்முடைய அன்றாட வாழ்வில் இந்த சூத்திரத்தின் பயனென்ன? பள்ளியில் படிக்கும் காலத்தில் கணிதம் கற்றுதரும் பொழுது அதன் நேரடி பயன்பாடு எப்படி நம் வாழ்வில் வருகிறது என்று சில சமயம் சிந்தித்ததுண்டு ஆனால் ஆசிரியரிடம் கேட்டதில்லை. சிக்கலான கணிதமும் நம் அன்றாட வாழ்வும் எனும் தலைப்பில் கட்டுரை இட வேண்டுகிறேன்.Formula என்பதற்கு சூத்திரம் என்பது சரியான மொழிபெயர்ப்பாய் இருக்கும் என நினைக்கிறேன். கணிதம் சார்ந்த தமிழ் கலைச்சொற்களுக்கு தமிழக அரசின் பாட நூல்களை அணுகுவதே சிறந்தது. என் வாழ்வில் பத்தாம் வகுப்புவரை கணிதத்தை தூய தமிழிலேயே கற்றேன்.
ReplyDelete
Replies
சார்வாகன்November 5, 2011 at 10:09 PM
/Data Entry வேலைகள் பணம் செலுத்தாமல் இலவசமாக கிடைக்கிறது !

/
நண்பர் ஆன்லைன் ஜாப்ஸ்
நீங்கள் சொல்வது உண்மையெறு எப்படி நம்புவது?.உங்களால் இதுவரை பலனடைந்த எவரையாவது அனைத்து விவரங்களுடன் பதிவிட சொல்லுங்கள்.
நன்றி
ReplyDelete
Replies
சார்வாகன்November 5, 2011 at 10:13 PM
நண்பர் நரேன்
நாம் கணிதம் கண்டுபிடித்தது ஏன் எனில் சோம்பல் பட்டு ஒரு வேலையை எளிதில் செய்யும் முயற்சியாக பரிணமித்ததே கணிதம்.!!!!!!!!!!!!

ஆகவே எப்ப்டி ஷார்ட் கட் தேடும் நண்பர்களுக்கு கணிதம் தானே வரும்.ஆகவே முதலில் சோம்பேறி ஆகிவிடுங்கள்.கணிதம் தானே வரும்!!!!!!.இது எப்படி?
Just for fun!!!!!!!!!!!!
நன்றி
ReplyDelete
Replies
சார்வாகன்November 5, 2011 at 10:20 PM
நண்பர் சீனிவாசன்
சூத்திரம் சரியான் சொல் எனவே நினைக்கிறேன். நன்றி.ஒரு விஷயத்தை தமிழில் கோர்வையாக ,குறிப்பிட்ட பொருள் மட்டுமே வரும் வகையில் மட்டுமே விளக்க இயல்கிறேன்.

அடிக்கடி வாருங்கள்.தேவையான மாற்றங்களை விமர்சியுங்கள்.
/சிக்கலான கணிதமும் நம் அன்றாட வாழ்வும் எனும் தலைப்பில் கட்டுரை இட வேண்டுகிறேன்/
நல்ல தலைப்பு. உண்மையில் நம் அன்றாட வாழ்வில் பல நிகழ்வுகள் மிகவும் சிக்கலானது . பல எளிமைப் படுத்தல்(assumtions) கொடுத்தே செய்ய முடியும் .தொடர் பதிவு தேவைப்படலாம். முயற்சிக்கிறேன்.
நன்றி
ReplyDelete
Replies
superlinksNovember 6, 2011 at 3:11 AM
வணக்கம், உங்களுக்கு இணைப்பு கொடுத்துள்ளேன் பாருங்கள்.
ReplyDelete
Replies
சார்வாகன்November 6, 2011 at 5:16 PM
நன்றி நண்பரே superlinks
ReplyDelete
Replies
தருமிNovember 6, 2011 at 7:35 PM
//முதலில் சோம்பேறி ஆகிவிடுங்கள்//

நான் எப்பவுமே அப்படித்தான்!

//உங்க மண்டை முழுக்க மூளையாகவே இருக்குமோ? எல்லா ஆழமான விசயகளிலும் கலந்து அடிக்கீறீங்க.//

எப்பவுமே உள்ள பொறாமையுடன் ... ஆமாம் .. ஆமாம்.
ReplyDelete
Replies
சார்வாகன்November 7, 2011 at 8:17 AM
நன்றி தருமி அய்யா
இணையத்தில் என்னை விட அதிகம் கற்றவர்கள்,அறிந்தவர்கள் இருந்தாலும் அவர்கள் (தமிழில்)எழுத முயற்சிக்காத ஒரே காரணத்தால் நான் செய்கிறேன் அவ்வளவுதான்.நமக்கு தெரிந்தது தேடல் அவ்வளவுதான்.இந்த பதிவுகளுக்கு கிடத்த பாராட்டுகளை ஒரு அங்கீகாரமாகவே கருதுகிறேன்.
இன்னும் நிறைய எழுத வேண்டியுள்ளது.

பணி&பயணம் கொஞ்சம் அதிகம் என்பதால் ஒரு 15 நாள் பதிவு வராது.பிறகு சந்திப்போம்.
நன்றி
ReplyDelete
Replies
வவ்வால்November 11, 2011 at 11:09 AM
சார்வாகான்,

நீங்க ரொம்ப ஆசிரியர் கணக்கா பாடம் நடத்துவதாலேயே பின்னூட்டம் போடமுடிவதில்லை :-))

ஆனாலும் கடந்த கால கணக்குகளை நியாபகப்படுத்தி தொந்தரவு பண்றிங்க.

சீனிவாசன் நடைமுறைல என்ன சம்பந்தம்னு கேட்டதால சொல்லிக்கிறேன்,
n(n+1)/2 இதை வச்சு தான் கிரிக்கெட் போன்ற போட்டிகளில் லீக் சுற்றில் எத்தனை மேட்ச் நடக்கும்னு கண்டு பிடிப்பாங்க, ராபின், ரவுண்டு ராபின் என இரண்டுக்கும் உதவும்.

இது போல எல்லாத்துக்கும் ஒரு நடைமுறை பயன்ப்பாடு இருக்கலாம்,நமக்கு தெரியாம இருக்கு அவ்வளவு தான். கன்னியாகுமரில இருக்க வள்ளுவர் சிலை கூட கணித சூத்திரம் வைத்து தான் செய்யப்பட்டது, தனி தனி கல்லில் பாகங்கள் செய்யப்பாட்டு இணைக்கப்பட்டது,ஆனாலும் சரியா பொருந்தி இருக்கும்.பிரமிட் இன்னொரு உதாரணம்.
ReplyDelete
Replies
ஷர்புதீன்November 18, 2011 at 1:47 PM
if u have time, tell me we chat about maths somewhile
ReplyDelete
Replies
சார்வாகன்November 19, 2011 at 6:52 AM
நண்பர் ஷர்புதீன்
கணிதத்தில் உங்களுக்கு பிடித்த தலைப்பை சொன்னால் அது குறித்து சில பதிவுகள் இடுகிறேன்.அதில் விவாதிப்போம்.இபோது பணி பளு காரணமாக இணையத்தில் நேரம் செலவிட முடிவது இல்லை.வருகைக்கும் கருத்து பதிவிற்கும் நன்றி.
ReplyDelete
Replies