Monday, September 3, 2012

தொடர் பின்னக் கூட்டல் அறிவோமா? Part 3



வணக்கம் நண்பர்களே,

சென்ற இரு பதிவுகளில் தொடர் பின்னக் கூட்டல் பற்றி அறிந்தோம் . இப்பதிவில் அதற்கும்  ஃபிபோனோசி  தொடருக்கும் உள்ள  தொடர்பு  மட்டும்  பார்த்து விடுவோம்.

ஃபிபொனோசி  தொடர் என்றால் சென்ற பதிவில் இறுதியில் இலேசாக கோடிட்டு காட்டி இருந்தோம்.வரலாறு, அறிவியலில் ஒரு விடயத்தின் மாற்றம் என்பது அதன் கடந்த கால நிலைகளை பொறுத்தது. அதற்கு கணிதத்தில் எ.கா எனில் ஃபிபோனோசி தொடர் சொல்லலாம். ஒரு தொடரின் இப்போதைய எண்,முந்தைய எண் இவற்றின் மூலம் அடுத்த எண்ணை கண்டுபிடிப்பதுதான் இது. அனைவரும் அறிந்த
எளிய ஃபைபோனோசி தொடர்
1,1,2,3,5,8,11,19,…..
அதாவது எந்த தொடர்ந்த  இரு எண்களைக்  கூட்டினாலும் அடுத்த எண் கிடைக்கும்.இதில் குறிப்பிடத்தக்க விடயம் என்னவெனில் அடுத்தடுத்த எண்களின் விகிதம் ஒரு குறிப்பிட்ட மதிப்பை நோக்கி செல்லும்,

S.No
Fibonocci Number
A(n-1)/A(n)
A(n)/A(n-1)
1
1
1
1
2
1
0.5
2
3
2
0.666666667
1.5
4
3
0.6
1.666666667
5
5
0.625
1.6
6
8
0.615384615
1.625
7
13
0.619047619
1.615384615
8
21
0.617647059
1.619047619
9
34
0.618181818
1.617647059
10
55
0.617977528
1.618181818
11
89
0.618055556
1.617977528
12
144
0.618025751
1.618055556
13
233
0.618037135
1.618025751
14
377
0.618032787
1.618037135
15
610
0.618034448
1.618032787
16
987
0.618033813
1.618034448
17
1597
0.618034056
1.618033813
18
2584
0.618033963
1.618034056
19
4181
0.618033999
1.618033963
20
6765



இங்கே மதிப்பு விகிதம்   A(n)/A(n-1) தங்க சராசரி விகிதம் எனப்படும்

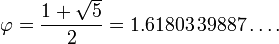
\varphi = \frac{1 + \sqrt{5}}{2} = 1.61803\,39887\dots.

<!--[if !vml]--><!--[endif]-->
http://en.wikipedia.org/wiki/Golden_ratio

சரி ஃஃபிபோனோசி தொடர் எனில் 

1.தொடர்ந்த இரு எண்களின் தொடர்பில் அடுத்த எண் வரும்.

2. அடுத்த எண்களின் விகிதம் ஒரு குறிப்பிட்ட மதிப்பை நோக்கி செல்லும்.

இதற்கும் தொடர் பின்னத்திற்கும் என்ன தொடர்பு?

மீண்டும் இரமானுஜம் தீர்வு கண்ட புதிருக்கு செல்ல வேண்டியதுதான்.

அப்புதிரின் விடை தொடர் பின்னம் என்பதையும் அதன் ஒவ்வொரு ஒருங்கும்[stage] தீர்வே என்பதை சென்ற பதிவுகளில் அறிந்தோம்.ஆனால் ஒவ்வொரு ஒருங்கையும் கணக்கிடுதல் அதிக வேலை தரும் செயல் ஆக இருப்பதால் ஒருங்கையும் ஃபிபோனோசி தொடர் மூலம் கணக்கிடலாம் என்பதுதன் இப்பதிவின் நோக்கம். 

ரமானுஜம் தீர்வு கண்ட புதிர்

x^2 - 10 y^2 = +1 or -1

  x,y=integers

ஆனால் இராமானுஜன்புதிரைக் கேட்டவுடனேயே, இதன் விடை ஒரு தொடர் பின்னத்தில் இருக்கிறது என்று கீழ்வரும் தொடர் பின்னத்தை சொன்னார்:

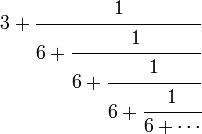
3 + \cfrac{1}{6+\cfrac{1}{6+\cfrac{1}{6+\cfrac{1}{6+\dotsb}}}}


புதிருக்கு தீர்வு காணும் முறை பகுதி இரண்டில் விள்க்கினாலும் மீண்டும் விள்க்குகிறோம்.

K =10 ஆகவே b=6

எப்படி???


b^2/4+1=K i.e -----6*6/4+1=10

'b/2=3' முழு எண்ணாகவும் b=6 தொடர் பின்னமாகவும் வரும் என்பதும் நாம் அறிந்ததே இபோது விடையை  பாருங்கள்.மலைப்பாக இருக்காது!!!

எனினும் ஒவ்வொரு ஒருங்கையும் ஃபைபோனோசி தொடராக எளிதாக  கணிப்பதே நாம் விரும்புகிறோம். 

கணிதம் கண்டுபிக்கப்பட்டதே நமது சோம்பலை வளர்க்கவே!!!

ஹி ஹி!!!!


சென்ற இரு பதிவும் புரியாதவர்கள் கூட இப்பதிவை புரிய முடியும். தீர்வு காண  கீழ்க்கண்டது போல் ஒரு கட்டங்கள் எக்செல்[excel] அல்லது காகிதத்திலோ வரையலாம்.
முதல் அடுக்கு(column) வரிசை எண் மட்டுமே.

இரண்டாம் அடுக்கு  தீர்வின்  'y' அளிக்கிறது .இது 'b=6' ன் மதிப்பு சார்ந்தது. 

மூன்றாம் அடுக்கு  தீர்வின்  'x' அளிக்கிறது .இது b/2=3 ன் மதிப்பு சார்ந்தது. 

கடைசி அடுக்கு தீர்வினை சோதித்து +1 அல்லது -1 வருகிறதா என சோதிக்கிறது.


 S.no
y…(b=6)x…(b/2=3)x^2-10y^2
ABx/yx^2/y^2
0 0
113-139
261913.16666710.02778
337117-13.1621629.99927
422872113.16228110.00002
514054443-13.1622789.999999
686582737913.16227810
753353168717-13.16227810
8328776103968113.16227810
920260096406803-1
3.16227810





முதல் தீர்வு A1= y=1 ,  B1=x=b/2=3

A2=b*A1+A0=6*1+0=6        B2=(b/2)*A2+A1=3*6+1=19

A3=b*A2+A1=6*6+1=37        B3=(b/2)*A3+A2=3*37+6=117

........
.........

A(n)=b*A(n-1)+A(n-2)               B(n)=(b/2)*A(n)+A(n-1)
x^2-y^2=+1 or -1 க்கான தீர்வும் அளிக்கிறோம்!!!
K=2 so b=2.....b^2/4+1=K...4/4+1=2

Y
‘b=2’
X
‘b/2=1’
x^2-2y^2
1
1
-1
2
3
1
5
7
-1
12
17
1
29
41
-1
70
99
1
169
239
-1
408
577
1
985
1393
-1



எளிதாக கணிப்பான் கொண்டோ எக்செல் சீட்டிலோ எளிதாக எந்த அளவு வேண்டுமோ கணக்கிடலாம். எக்செல் சீட்டில் 10 தசம இடம்[decimals] மட்டுமே வருவதால் அதிக தீர்வுகள் வேண்டுபவர்கள் முழு எண் தீர்வுக்கு வேறு அறிவியல் மென்பொருள் பயன்படுத்த வேண்டும். எனினும் இதே முறையே பலன் அளிக்கும்.

ஆகவே புதிரில் K ன் மதிப்பு அறிந்து 'b' கணித்து மேலே சொன்ன கட்டம் ஃபிபோனோசி தொடர்போல் சூத்திரம் கொண்டு எழுதினால் ஒருங்குகள் எளிதில் கணக்கிடலாம்.

கேள்விகளை தயக்கமின்றி கேட்க வேண்டுகிறேன்!!!

நன்றி நன்றி நன்றி!!!!!!!!


Some more information for interested.!!

Pi Continued Fraction



http://mathworld.wolfram.com/PiContinuedFraction.html
Posted by at
Labels: ,

9 comments:

  1. டி.என்.முரளிதரன் -மூங்கில் காற்று September 3, 2012 at 5:31 AM

    கொஞ்சம் புரிந்தும் புரியாதது மாதிரி இருக்குது. இன்னும் ஒரு தடவை படிச்சிட்டு வரேன் பாஸ்

    ReplyDelete
  2. சார்வாகன்September 3, 2012 at 6:34 AM

    வாங்க சகோ முரளி,
    கொஞ்சம் எழுதிப் பார்த்தால் பிடிபட்டு விடும்.
    நன்றி

    ReplyDelete
  3. UnknownSeptember 3, 2012 at 1:37 PM

    வணக்கம் சகோ.'சார்'வாகன்,
    //கணிதம் கண்டுபிக்கப்பட்டதே நமது சோம்பலை வளர்க்கவே!!!

    ஹி ஹி!!!!//

    அதைவிட கால்குலேட்டர்(வவ்வால் கிட்ட தமிழில் கேட்டுவிட்டு சொல்கிறேன்)கண்டுபிடிக்கப்பட்டதே சோம்பலோ சோம்பலை வளர்க்கவே!!!ஹி..ஹி....
    கணக்கு ரொம்ப பின்னுது சகோ.இருந்தாலும் ஒரு முறைக்கு இருமுறை படித்துவிடுகிறேன்.நன்றி!!!

    இனியவன்....

    ReplyDelete
  4. சார்வாகன்September 3, 2012 at 7:15 PM

    வாங்க சகோ இனியவன்,

    இப்பதிவில் கூறி இருப்பது மிக மிக எளிமையான விடயம்.

    பாருங்கள் இந்த புதிருக்கு தொடர்சியான் தீர்வு ஒருங்குகள் கண்டுபிடிக்க வேண்டும்
    x^2-2y^2=+1 or -1
    K=2 so b =2 how
    b^2/4+1=K.... 4/4+1=2

    முதல் தீர்வு ஒருங்கு x=b/2,y=1 என்பதல் x=1 y=1

    y=[1,1,2,5,12,29......]

    x=[1,2,3,7,17,41.....]


    y... x... x^2-2y^2
    1.. 1.. -1
    2... 3... 1
    5.. 7... -1
    12 17 1
    29 ....41... -1
    70... 99... 1
    169... 239... -1
    408... 577... 1
    985 ... 1393... -1


    நன்றி!!!!!!!!!!

    ReplyDelete
  5. narenSeptember 5, 2012 at 2:08 PM

    சகோ. சார்வாகன் நலமா,

    முதலில், இராமனுஜம் எந்த ஐ.ஐ.டியில் படித்தார்??? :)))

    தொடர் பின்னக் கூட்டல் தொடர், கணித அறிவிலியான என் போன்றவர்களுக்கு, தொபிகூ பற்றிய அறிமுகம் கிடைத்தது. சில நண்பர்கள் சமன்பாடுகளை பார்த்தவுடன், கிரேக்கமாக இருக்கின்றது என ஓடிவிட்டனர். கணிதம் தெரியாதவர்கள் நினைத்துக்கொள்வது (assumption) செய்யமுடியாததால், புரிந்து கொள்வது கடினமாக இருக்கும். அதனால் சிறுபிள்ளை போல் அனைத்தும் கேட்டால் விளங்கிவிடும் என நினைக்கிறேன்.

    x^2-10y^2 = +1 or -1 என்ற விடை வரவேண்டிய x அல்லது y யின் எண் என்ன?

    கேள்வி.மஹலனொபிஸ்க்கு, இந்த சமன்பாட்டை பற்றிய கேள்வி வர வேண்டிய அவசியம் என்ன? இந்த சமன்பாட்டிற்கு ஏதாவது தனிசிறப்பு உண்டா?

    விடை தரக்கூடிய x மற்றும் y யின் எண்கள் முதலில் 3 மற்றும் 1 இரண்டாவது 19 மற்றும் 6 மூன்றாவது 117 மற்றும் 37 என்று முடிவில்லாமல் போய் கொண்டேயிருக்கும். இந்த எண்கள் இராமனுஜத்தின் தொடர்பின்னத்தின் மூலம் அறியமுடியும்.

    இந்த தொடர்பின்னத்தை இராமனுஜம் எப்படி கண்டுபிடித்தார், சமன்பாடுகளை அளித்தாரா (6 ஆம் எண் எப்படி வந்தது)? இருசம்னபாட்டிற்கு நான் ஏன் செல்ல வேண்டும், தொடர்பின்னத்திற்கும் இதற்கு என்ன சம்பந்தம்.

    நன்றி தொடரும்.

    ReplyDelete
  6. சார்வாகன்September 5, 2012 at 6:02 PM

    வணக்கம் சகோ நரேன்,

    நலமா?? கொஞ்ச நாள் ஆளைக் காணவில்லை?? அடிகடி ப்திவு,பின்னூட்டம் இட வேண்டுகிறேன்.

    சரி பதிவுக்கு போவோம். முதலில் தொடர்பின்னம் என்ற அமைப்பை பயன்படுத்தியவர் நமது முப்பாட்டன் திரு ஆர்யபட்டா அவர்களே[பொ.ஆ 5ஆம் நூற்றாண்டு]. நேர்மாறி சமன்பாடுகளைத் தீர்க்க,'பை' மதிப்பு கண்டறிய என பல விடயங்கள்க்கு பயன்படுத்தினார். தொடர்பின்ன பகுதி 1 ல் அவரின் புத்தகம் கூட தரவிற்க்க பின்னூட்டத்தில் சுட்டி அளித்து இருக்கிறேன் .
    கேள்வி கேட்பது என்பது மிகவும் நல்ல விடயம். கேள்வி கேட்க கேட்கவே சரியாக புரிதல்,விளங்குதல் சார் கற்றல் செய்ய இயலும்.ஒரு சரியா கேள்வியில் பாதி விடை உண்டு.பதிலும் கிடைகும். சிலசமயம் விடை இல்லை என்பதோ, பல் விடைகளோ கூட இருக்க்லாம என்பதே சரியான பன்முகப் பார்வை !!!
    *****************
    இப்போது உங்கள் கேள்விகளுக்கு வருகிறேன்.


    1/x^2-10y^2 = +1 or -1 என்ற விடை வரவேண்டிய x அல்லது y யின் எண் என்ன?/

    தீர்வுகளை கலப்பு பின்ன்மாக எழுதுகிறேன். தீர்வு=x/y பகுதி=x தொகுதி=7
    முதல் தீர்வு=x1/y1=3/1...
    இரண்டாம் தீர்வு x2/y2= 19/6
    மூன்றாம் தீர்வு=x3/y3=117/37

    இப்பதிவில் தொடர்ச்சியான பகுதிகள்,தொகுதிகள் இடையே உள்ள தொடர்பு ஃபைபோனோசி தொடர் போன்றது என எளிய முறையில் கண்க்கிடலாம் என்பதையே விள்க்குகிறோம்!.
    Equation

    x^2-K.y^2=+1 or -1

    'b'ன் மதிப்பு 'K' ல் இருந்து கண்டுபிடிக்கலாம்

    b^2/4+1=K

    if K=10 then b^2/4+1=10....b^2=36...b=6!!!

    கண்டுபிடித்த பின் தொடர்ச்சியாக தீர்வுகள் ஃபைபோனோசி தொடர்போல் சுழல்நிலை சமன்பாடுகள்[recursive equations] மூலம் கண்டறியலாம்.

    y(n)=b*y(n-1)+y(n-2)

    x(n)=(b/2)*y(n)+y(n-1)
    தொடர்பின்னமக் கூட்டுவதை விட முழு எண்களாக தீர்வுகாண்பது இம்முறையில் எளிது!!.

    நன்றி
    (தொடரும்)

    ReplyDelete
  7. சார்வாகன்September 5, 2012 at 6:13 PM

    2.//கேள்வி.மஹலனொபிஸ்க்கு, இந்த சமன்பாட்டை பற்றிய கேள்வி வர வேண்டிய அவசியம் என்ன? இந்த சமன்பாட்டிற்கு ஏதாவது தனிசிறப்பு உண்டா?//

    3/இந்த தொடர்பின்னத்தை இராமனுஜம் எப்படி கண்டுபிடித்தார், சமன்பாடுகளை அளித்தாரா (6 ஆம் எண் எப்படி வந்தது)? இருசம்னபாட்டிற்கு நான் ஏன் செல்ல வேண்டும், தொடர்பின்னத்திற்கும் இதற்கு என்ன சம்பந்தம்.//

    சகோ நரேன்,
    தொடர்பின்னம் என்பது மிகப் பழமையானது.இரமானுஜம் அதில் சில பங்களிப்பு செய்து உள்ளார். சென்ற கேள்வியின் தொடக்கத்தில் இதற்கு பதில் சொல்லி இருக்கிறேன் என்றாலும் கொஞ்சம் சுட்டிகள் அளித்தால் அதிக விளக்கம் பெறுவீர்கள்.

    http://archives.math.utk.edu/articles/atuyl/confrac/history.html

    The origin of continued fractions is hard to pinpoint. This is due to the fact that we can find examples of these fractions throughout mathematics in the last 2000 years, but its true foundations were not laid until the late 1600's, early 1700's.

    The origin of continued fractions is traditionally placed at the time of the creation of Euclid's Algorithm.[6] Euclid's Algorithm, however, is used to find the greatest common denominator (gcd) of two numbers.
    ****
    http://mathoverflow.net/questions/49866/applications-of-finite-continued-fractions

    http://fora.tv/2010/11/16/Gresham_Professor_John_Barrow_Continued_Fractions

    இதில் பல் முனைவர் பட்ட ஆய்வுகளே நடக்கும் அளவுக்கு சரக்கு [ஹி ஹி இது வேற!]இருக்கிறது.நாம் ஒரு குறிப்பிட்ட வகை தொ.பி அதுவும் ஒரு புதிர் தீர்க்கும் அள்வு மட்டுமே கோடிட்டு காட்டினோம்,அவ்வளவுதான்!!

    நன்றி

    ReplyDelete
  8. narenSeptember 5, 2012 at 6:35 PM

    சகோ.
    ///
    கொஞ்ச நாள் ஆளைக் காணவில்லை?? அடிகடி ப்திவு,பின்னூட்டம் இட வேண்டுகிறேன்.///

    இணைய வசதியில்லாத கிராமங்கள் இன்னும் தமிழ்நாட்டில் இருக்கின்றன.

    விளக்கங்களுக்கு நன்றி, பிடிபட ஆரம்பிக்கிறது.

    ReplyDelete
  9. சார்வாகன்September 5, 2012 at 6:55 PM

    சகோ நரேன்,
    பிடிபட்டுவிடும். அனைவருக்கும் எளிதில் எதையும் புரிய வைக்க முடியும் என்பதே நம் கொள்கை. இதில் கற்பவரின் நேரம்,முயற்சி,ஈடுபாடு சார்ந்தே 99% கற்றல் உள்ள‌து.

    எனினும் ஆசிரியர் தினத்தில் புதிதாக் கற்றல் செய்து உள்ளீர்கள். வாழ்த்துக்கள்.

    நம்மை உருவாக்கிய கல்விச்சாலை&பதிவுலக துரோணர்களுக்கு இந்த ஏகலைவனின் ஆசிரியர் தின வாழ்த்துக்கள்!!

    சார்வாகன்

    ReplyDelete

Subscribe to: Post Comments (Atom)