வணக்கம் நண்பர்களே,
நாம் மக்களுக்கு பயன்படும் அறிவியல்,கணிதம் ,இயற்கை மேம்பாடு போன்றவற்றில் ஈடுபாடு கொண்டு இது குறித்த கற்றலை பகிர்ந்து வருகிறோம். பெரும்பாலான கணிதப் பதிவுகளில் பின்னூட்டமிடும் சகோக்கள் இதற்கு பயன் பாடு எளிதில் அறியும் வண்ணம் உண்டா எனவே கேட்பார்கள்.
நமக்கு அனைத்துக்கும் எளிய முறையில் பயன்பாடு கூற முடியாமல் போவதால் வருத்தம் உண்டு.அப்படி இருக்கும் போது ட்யூக்[Duke] பல்கலைகழகம் பல இலவச பாடங்கள் வழங்குவதும் அது குறித்த பரிணாம கல்வி குறித்தும் ஒரு பதிவிட்டோம் என்பது ஞாபகம் வந்தது.அத்தளத்தில் இன்னும் பல துறை சார் இலவச கல்விகள் உண்டு. அதில் கணக்கீட்டு நிதியியல்[Computational Finance] குறித்த ஒரு உரை கேட்டேன்.
அது வட்டி கணக்கிடுதல் பற்றிய விளக்க உரை ஆகும். அதில் வகைக்கெழு பயன்பாடும் இடம் பெற்றது ஆகா "கண்டேன் வட்டியில் வகைக்கெழுவின் பயன்பாட்டை" என ஆர்க்கிடிமஸ் போல் யுரேகா[ ஹி ஹி நான் அப்போது குளித்துக் கொண்டு இருக்கவில்லை] என கத்திக் கொண்டு ஓட வேண்டும் போல் இருந்தது.
சரி புல்லரித்தது போதும்.ஒவ்வொருவருக்கும் ஈடுபாடுள்ள ஒவ்வொரு விடயத்தில் புல்லரிப்பு[?!] நிகழ்கிறது என்பதால் பதிவுக்கு செல்வோம்.
பெரும்பான்மை மனிதர்களுக்கு வட்டி கணக்கீடு என்பது ஒரு இன்றியமையா விடயமே. வட்டி என்பது என்ன?
நாம் ஒவ்வொரு விடயத்திலும் வலியுறுத்தும் அடிப்படை விடயம் ஒன்றே ஒன்றுதான்!!!
"மாற்றம் ஒன்றே மாற்றம் இல்லாதது"
இதன் அடிப்படையில் அனைத்தையும் அறிய, புரிய,கற்க முயல்வதே சரியான பன்முக பார்வையாக நாம் ஏற்கிறோம்.
சரி வட்டி என்றால் சரியான வரையறுப்பு என்ன?
When money is borrowed, interest is typically paid to the lender as a percentage of the principal, the amount owed to the lender. The percentage of the principal that is paid as a fee over a certain period of time (typically one month or year) is called the interest rate.
ஒரு பொருளை பயன்படுத்துவதற்கான அதன் உரிமையாளருக்கு செலுத்தப்படும் பணம்.இது பொதுவாக பணம் கடனாக வாங்கி திருப்பி செலுத்தும் போது கொடுக்கப்படும் உபரி பணம் என்பதையே குறிக்கிறது. இது கடனாக வாங்கிய பணம் இதன் பெயர் 'முதலீடு[மூலதனம்,Principal Amount]' ன் மதிப்பில் குறிப்பிட்ட பங்கு[பாகம் அல்லது சதவீதம்] ஆகும்
இன்னும் நம் பாணியில் சொல்வது என்றால் "காலரீதியான பண மதிப்பின் மாற்றம்" என்பதே சரியான வரையறுப்பு.இது அதிகரிப்பதாகவே ஏற்கப் பட்டாலும் சில விதி விலக்குகள் உண்டு.இப்போது வட்டிக் கண்க்கீட்டில் நுண்கணிதம் பயன்பாடு வருவதை மட்டும் விளக்குவோம்.
மூலதனத்தை பயன்படுத்துவதற்கான வாடகை வட்டிவீதம்[interest rate] என்ப்படுகிறது.பெரும்பாலும் இது ஆண்டுக்கு என வரையறுக்கப்படுகிறது. கணக்கீட்டில் மூலதனம், காலம், வட்டி வீதம் இந்த மூன்றும் காரணிகள் ஆகும்.
முதல்[மூலதனம்,அசல்] என்பதை 'PV[Principal Value]'என்போம்
வட்டி வீதம் என்பதை 'R' என்போம்
காலம் என்பதை 't'ஆண்டுகள் என்போம்.
இப்போது வட்டியில் இருமுறை உண்டு 1.எளிய வட்டி,2. கூட்டு வட்டி
PV என்ற மூலதனம் 't' ஆண்டுகளுக்கு பின் அடையும் மதிப்பை 'FV' (Final Value] என்போம்.
100 ரூபாய் 10% வட்டிவீதத்தில் 5 வருடத்தில், பல வட்டி கணக்கீட்டு முறைகளின் படி எவ்வள்வு ஆகிறது என்பதை எ.கா ஆக கொள்வோம்.
PV=100
100 ரூபாய் 10% வட்டிவீதத்தில் 5 வருடத்தில், பல வட்டி கணக்கீட்டு முறைகளின் படி எவ்வள்வு ஆகிறது என்பதை எ.கா ஆக கொள்வோம்.
PV=100
t=5
R=10%
A) முதலில் எளிய வட்டி கணக்கிட கற்போம்!!
FV=PV*[1+t*R]
FV=100*[1+5*10/100]=100*1.5=150Rs
வருடத்திற்கு 10 ரூபாய் என்ற வீதத்தில் 5 வருடத்தில் 50 ரூபாய் முதலீடு 100 ரூபாய் உடன் சேர்ந்து 150 ஆனது.இதில் வட்டி என்பது முதலீடு உடன் எப்போதும் சேராது. இப்படி வெளிப்படையிலான எளிய முறை பெரும்பானமை வங்கிகளில் பயன்படுத்துவது இல்லை!!!.
***********
B)இப்போது கூட்டு வட்டி கணக்கிட கற்போம்.
இப்போது என்ன வித்தியாசம் எனில் வட்டி மூலதனத்துடன் சேர்ந்து விடுகிறது.

FV=100*(1+0.10)^5= 161.05 Rs
பாருங்கள் கூட்டு வட்டியில் வட்டி குட்டி போடுவ்தை 150 ரூபாய்க்கும்,
161 ரூபாய்க்கும் உள்ள வித்தியாசத்தை.
கூட்டு வட்டியும் அதிகம் என்றாலும் குறைந்த பட்சம் வெளிப்படையான வட்டி
கணகீட்டு முறைதான். பல்முறை வங்கி வட்டிகளில் நாம் கணக்கிட்ட அளவுக்கும்,
வங்கி அளவுக்கும் வித்தியாசம் இருக்கும் ஏன் என்றால் பல வங்கிகள்
தொடர் கூட்டு வட்டி [Continuous Compound Rate] என்னும் முறையை பின்பற்றுகின்றன.
இது என்னவெனில் வருட வட்டி 10% என்றாலும் இது ஒரு வருடத்தில் எத்தனை முறை கண்க்கிடப்படும் என்பதை சொல்ல மாட்டார்கள். வருடத்திற்கு இரு முறை அதாவது ஆறுமாதத்திற்கு ஒரு முறை 5% கூட்டு வட்டி முறையில் கணக்கிட்ட்டால் வட்டி எவ்வள்வு மாறுகிறது.
PV=100
t=2*5=10
r=10/2=5%
n=2[வருடத்திற்கு இரு முறை]
FV=PV*(1+r/n)^(n*t)
FV=100*(1+0.05)^10=162.88Rs
மாதம் ஒரு முறை கண்க்கிட்டால் எவ்வளவு மாறும்?
n=12[மாதம் ஒரு முறை]
FV=100*(1+0.1/12)^60=164.5 Rs
ஆஹா அப்போது ஒரே வருட வட்டி வீதத்தில் ,இடையிடையே அதிக முறை கண்க்கிட்டால் வட்டி அதிகம் வருகிறதே. இதுதான் பலமுறை வட்டி வித்தியாசம் நமது,வங்கி கண்கீடுகளில் வருவதன் காரணம் ஆகும்.
சரி இது அதிக பட்சம் எவ்வளவு வரை போகும்? அதாவது ஒரு வருடத்தில் குறிப்பிட்ட வருட வட்டி வீதத்தில் ,முடிவிலி[infinite] முறை வட்டி கணக்கிட்டால் எவ்வளவு அதிகம் ஆகும்?
முடிவிலி முறை செய்ய முடியுமா ? ஏன் இப்படி விதண்டாவாதம் பேசுகிறீர் சகோ என்கிறீர்களா?
என்ன செய்வது?
n= முடிவிலி என்று சூத்திரத்தில் பிரதி இட்டால்[substitute] நம்மால் நேரடியாக கணக்கிட இயலாது. ஆகவே இதற்கு நுண்கணிதம்[Calculus] பயன்படுத்த வேண்டும்.
இந்த தொகை நுண்கணிதம் என்பதே பூச்சியம்,முடிவிலி சார் கணக்கீடு என்றால் ஒத்துக் கொள்வீர்களா?
சும்மா அடித்து விடாதீர்கள். இப்படியே உளறுவதே உமக்கு வாடிக்கை,நாங்கள் படித்த புத்தகம் எதுவும் இப்படி சொல்லவில்லை. எந்த சங்கப் பாடலில் மன்னிக்கவும் ஆய்வுக் கட்டுரையில்,புத்தகத்தில் இப்படி உள்ளது? நிரூபிக்க முடியுமா? நேருக்கு நேர் ஒத்தைக்கு ஒத்தை விவாதம்[மட்டுமே ஹி ஹி] வர்ரீயா என பல மனக்குரல்களை நம்மால் [ ஹி ஹி காதில் அல்ல!!] கேட்க முடிகிறது.
வகைக்கெழு என்றால் என்ன சொல்வோம் ஒரு மாறித் தொடர்பின் மிகச் சிறு மாறு விகிதம்[ rate of change of a function]. இது குறித்து நம் முநதைய பதிவில் படியுங்கள்.
http://aatralarasau.blogspot.com/2011/10/differential-equations-1.html
ஒன்றுமில்லாமை[nothing], முழுமைத்துவம்[everything] இரண்டுமே தொடர்புடையவை.
கணிதத்தில் இது நன்கு புலப்படும்.
1/0=முடிவிலி, 1/முடிவிலி=0
எந்த எண்ணையும் அதே எண்ணால் வகுத்தால் விடை ஒன்று ஆனால் பூச்சியம்,முடிவிலி இரண்டும் அதற்கு விதி விலக்கு!!.ஏன் இப்படி
சிந்திக்க மாட்ட்டீர்களா ??????????/
ஏன் எனில் பூச்சியம் என்பதும்,முடிவிலி என்பது பலப் பல எண்கள்!!!!!!!!!!
எண்ணற்ற பூச்சியங்கள்,முடிவிலிகள் உண்டு!!!
இது குறித்து பின்னூட்டத்தில் அதிகம் விளக்குகிறேன்.
சரி வட்டிக் கணக்கிற்கு செல்வோம்.
எங்கே நிறுத்தினோம்?.
தொடர் கூட்டு வட்டி முடிவிலி காலத்திற்கு எப்படி கணக்கிடுவது?
இதற்கு எல் ஹாஸ்பிடல் கணித விதியை பயன்படுத்த வேண்டும். அதாவது சில விகிதங்கள் 0/0 அல்லது முடிவிலி/முடிவிலி என வந்தால், பகுதியை[numerator],தொகுதிகளை[denominator] தனித்தனியாக வகைக்கெழு[derivative] கண்ட பிறகு பிரதியிட்டு மதிப்பு பெறும் விதம் ஆகும். இது ஒன்றுக்கு மேற்பட்ட முறைகளும் செய்யலாம்.
f(x) =sin(x)/x
x=0,எனில்
f(x)=0/0
ஹாஸ்பிடல் விதியை பயன்படுத்தினால் பகுதி(மேலே), தொகுதி(கீழே) தனித்தனியாக வகைக்கெழு கண்டால்
sin(x) ன் வகைக்கெழு=cos(x),
(x) ன் வகைக்கெழு=1
sin(x)/x=cos(x)/1=cos(x) =cos(0)=1!!!!!!!!!
************
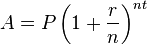
தொடர் கூட்டு வட்டியில் வருட பங்கீடு(n!!!) முடிவிலியாக இருந்தால் முதலீடு எப்படி வளரும் என்பதை அறிய முயல்வோம்.
இயற்கை மடக்கை[natural logirthm] எடுப்போம்!!
F= ln(K)
இயற்கை மடக்கை என்றால் 'e' ன் அடிப்படையில் காணுவதே. .இது ஒரு விகிதமுறா எண்[irrational number]. அதிக விடயங்களுக்கு விக்கி பிடியா காண்க!!
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828. The natural logarithm is generally written as ln(x),
loge(x)
பகுதி ,தொகுதி போல் வந்தால் மட்டுமே எல் ஹாஸ்பிடல் விதி பயன்படுத்த முடியும் என்பதால் கொஞ்சம் மாற்றி எழுதுகிறோம்!.
இப்போது பகுதி, தொகுதி தனித் தனியாக வகைக்கெழு காண
தொடர் கூட்டு வட்டி முறையில் முதலீடு வளரும் வீத சூத்திரம்
The formula for continous compound interest is given below
மீண்டும் ஒருமுறை ஞாபகப் படுத்துவோம்!!!
ஆகவே இப்பதிவில் எளிய வட்டி, கூட்டு வட்டி, தொடர் கூட்டு வட்டி என்பதை அறிந்தோம்.இன்னும் தொடர் கூட்டு வட்டியில் நுண்கணிதம் மூலம் சூத்திரம் காண்வும் கற்றோம்!!! முதலீடு 100 ரூபாய், 10% வருட வட்டிவீதத்தில் 20 வருடம் வரை எப்படி அதிகரிக்கிறது என்பதைக் காட்டும் படம்.
இக்காணொளியில் நாம் சொன்னது அனைத்தும் விள்க்குகிறார்.
நன்றி!!!!!!!!!!!!!
PV=100
t=2*5=10
r=10/2=5%
n=2[வருடத்திற்கு இரு முறை]
FV=PV*(1+r/n)^(n*t)
Where,
- A = final amount
- P = principal amount (initial investment)
- r = annual nominal interest rate (as a decimal, not in percentage)
- n = number of times the interest is compounded per year
- t = number of years
FV=100*(1+0.05)^10=162.88Rs
மாதம் ஒரு முறை கண்க்கிட்டால் எவ்வளவு மாறும்?
n=12[மாதம் ஒரு முறை]
FV=100*(1+0.1/12)^60=164.5 Rs
ஆஹா அப்போது ஒரே வருட வட்டி வீதத்தில் ,இடையிடையே அதிக முறை கண்க்கிட்டால் வட்டி அதிகம் வருகிறதே. இதுதான் பலமுறை வட்டி வித்தியாசம் நமது,வங்கி கண்கீடுகளில் வருவதன் காரணம் ஆகும்.
சரி இது அதிக பட்சம் எவ்வளவு வரை போகும்? அதாவது ஒரு வருடத்தில் குறிப்பிட்ட வருட வட்டி வீதத்தில் ,முடிவிலி[infinite] முறை வட்டி கணக்கிட்டால் எவ்வளவு அதிகம் ஆகும்?
முடிவிலி முறை செய்ய முடியுமா ? ஏன் இப்படி விதண்டாவாதம் பேசுகிறீர் சகோ என்கிறீர்களா?
என்ன செய்வது?
n= முடிவிலி என்று சூத்திரத்தில் பிரதி இட்டால்[substitute] நம்மால் நேரடியாக கணக்கிட இயலாது. ஆகவே இதற்கு நுண்கணிதம்[Calculus] பயன்படுத்த வேண்டும்.
இந்த தொகை நுண்கணிதம் என்பதே பூச்சியம்,முடிவிலி சார் கணக்கீடு என்றால் ஒத்துக் கொள்வீர்களா?
சும்மா அடித்து விடாதீர்கள். இப்படியே உளறுவதே உமக்கு வாடிக்கை,நாங்கள் படித்த புத்தகம் எதுவும் இப்படி சொல்லவில்லை. எந்த சங்கப் பாடலில் மன்னிக்கவும் ஆய்வுக் கட்டுரையில்,புத்தகத்தில் இப்படி உள்ளது? நிரூபிக்க முடியுமா? நேருக்கு நேர் ஒத்தைக்கு ஒத்தை விவாதம்[மட்டுமே ஹி ஹி] வர்ரீயா என பல மனக்குரல்களை நம்மால் [ ஹி ஹி காதில் அல்ல!!] கேட்க முடிகிறது.
வகைக்கெழு என்றால் என்ன சொல்வோம் ஒரு மாறித் தொடர்பின் மிகச் சிறு மாறு விகிதம்[ rate of change of a function]. இது குறித்து நம் முநதைய பதிவில் படியுங்கள்.
http://aatralarasau.blogspot.com/2011/10/differential-equations-1.html
ஒன்றுமில்லாமை[nothing], முழுமைத்துவம்[everything] இரண்டுமே தொடர்புடையவை.
கணிதத்தில் இது நன்கு புலப்படும்.
1/0=முடிவிலி, 1/முடிவிலி=0
எந்த எண்ணையும் அதே எண்ணால் வகுத்தால் விடை ஒன்று ஆனால் பூச்சியம்,முடிவிலி இரண்டும் அதற்கு விதி விலக்கு!!.ஏன் இப்படி
சிந்திக்க மாட்ட்டீர்களா ??????????/
ஏன் எனில் பூச்சியம் என்பதும்,முடிவிலி என்பது பலப் பல எண்கள்!!!!!!!!!!
எண்ணற்ற பூச்சியங்கள்,முடிவிலிகள் உண்டு!!!
இது குறித்து பின்னூட்டத்தில் அதிகம் விளக்குகிறேன்.
சரி வட்டிக் கணக்கிற்கு செல்வோம்.
எங்கே நிறுத்தினோம்?.
தொடர் கூட்டு வட்டி முடிவிலி காலத்திற்கு எப்படி கணக்கிடுவது?
இதற்கு எல் ஹாஸ்பிடல் கணித விதியை பயன்படுத்த வேண்டும். அதாவது சில விகிதங்கள் 0/0 அல்லது முடிவிலி/முடிவிலி என வந்தால், பகுதியை[numerator],தொகுதிகளை[denominator] தனித்தனியாக வகைக்கெழு[derivative] கண்ட பிறகு பிரதியிட்டு மதிப்பு பெறும் விதம் ஆகும். இது ஒன்றுக்கு மேற்பட்ட முறைகளும் செய்யலாம்.
f(x) =sin(x)/x
x=0,எனில்
f(x)=0/0
ஹாஸ்பிடல் விதியை பயன்படுத்தினால் பகுதி(மேலே), தொகுதி(கீழே) தனித்தனியாக வகைக்கெழு கண்டால்
sin(x) ன் வகைக்கெழு=cos(x),
(x) ன் வகைக்கெழு=1
sin(x)/x=cos(x)/1=cos(x) =cos(0)=1!!!!!!!!!
************
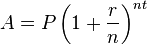
தொடர் கூட்டு வட்டியில் வருட பங்கீடு(n!!!) முடிவிலியாக இருந்தால் முதலீடு எப்படி வளரும் என்பதை அறிய முயல்வோம்.
இயற்கை மடக்கை[natural logirthm] எடுப்போம்!!
F= ln(K)
இயற்கை மடக்கை என்றால் 'e' ன் அடிப்படையில் காணுவதே. .இது ஒரு விகிதமுறா எண்[irrational number]. அதிக விடயங்களுக்கு விக்கி பிடியா காண்க!!
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828. The natural logarithm is generally written as ln(x),
loge(x)
பகுதி ,தொகுதி போல் வந்தால் மட்டுமே எல் ஹாஸ்பிடல் விதி பயன்படுத்த முடியும் என்பதால் கொஞ்சம் மாற்றி எழுதுகிறோம்!.
இப்போது பகுதி, தொகுதி தனித் தனியாக வகைக்கெழு காண
n=முடிவிலி என பிரதியிட
F=rt
தொடர் கூட்டு வட்டி முறையில் முதலீடு வளரும் வீத சூத்திரம்
The formula for continous compound interest is given below
மீண்டும் ஒருமுறை ஞாபகப் படுத்துவோம்!!!
ஆகவே இப்பதிவில் எளிய வட்டி, கூட்டு வட்டி, தொடர் கூட்டு வட்டி என்பதை அறிந்தோம்.இன்னும் தொடர் கூட்டு வட்டியில் நுண்கணிதம் மூலம் சூத்திரம் காண்வும் கற்றோம்!!! முதலீடு 100 ரூபாய், 10% வருட வட்டிவீதத்தில் 20 வருடம் வரை எப்படி அதிகரிக்கிறது என்பதைக் காட்டும் படம்.
P(principal)
|
Time(Years)
|
S.I
|
C.I
|
C.C.I
|
100
|
1
|
110
|
110
|
110.5159
|
100
|
2
|
120
|
121
|
122.1377
|
100
|
3
|
130
|
133.1
|
134.9817
|
100
|
4
|
140
|
146.41
|
149.1763
|
100
|
5
|
150
|
161.051
|
164.8636
|
100
|
6
|
160
|
177.1561
|
182.2005
|
100
|
7
|
170
|
194.8717
|
201.3607
|
100
|
8
|
180
|
214.3589
|
222.5356
|
100
|
9
|
190
|
235.7948
|
245.9374
|
100
|
10
|
200
|
259.3742
|
271.8
|
100
|
11
|
210
|
285.3117
|
300.3823
|
100
|
12
|
220
|
313.8428
|
331.9704
|
100
|
13
|
230
|
345.2271
|
366.8802
|
100
|
14
|
240
|
379.7498
|
405.4611
|
100
|
15
|
250
|
417.7248
|
448.0992
|
100
|
16
|
260
|
459.4973
|
495.2211
|
100
|
17
|
270
|
505.447
|
547.2983
|
100
|
18
|
280
|
555.9917
|
604.8519
|
100
|
19
|
290
|
611.5909
|
668.4577
|
100
|
20
|
300
|
672.75
|
738.7524
|
இக்காணொளியில் நாம் சொன்னது அனைத்தும் விள்க்குகிறார்.
நன்றி!!!!!!!!!!!!!






சகோ. நீங்கள் கணக்கு வாத்தியாராக ஆக வேண்டியவர்.. இந்த வட்டிக் கணக்கு எல்லாம் எனக்கு செமையாக குழப்பும் ! இன்றைக்குத் தான் ஓரளவு புரிந்துக் கொண்டுள்ளேன். அதிலும் நீங்கள் தமிழில் தந்த விதம் அருமை ( எங்கிருந்து தான் தமிழ் சொற்களை துலாவி எடுக்கின்றீர்களோ ஹிஹி ) ...
ReplyDeleteஎனக்கு இந்த கிரெடிட் கார்ட் வட்டி கொஞ்சம் குழப்பமாக இருக்கும், அதுக் குறித்தும் ஒரு பதிவு எழுதினால் தேவ'ல ! கிரெடிட் கார்ட் வட்டி கட்டியே நான் நாசாமாக போகின்றேன் !!!
வாங்க சகோ இ.செ
Deleteகடன் அட்டை கண்க்கு நாள் கணக்கில் தொடர் கூட்டு வட்டி கண்க்க்டப்படுகிறது. ஆகவே வருட,மாத வட்டியை விட அதிகமாகவே இருக்கும்.எனினும் பல ஏமாற்று வேலைகளும் நடப்பதால் நாம் கண்க்கிடும் அளவை விட வங்கி கண்க்கிடும் அள்வு அதிகமாகவே இருக்கும்
http://en.wikipedia.org/wiki/Credit_card_interest
Most U.S. credit cards are quoted in terms of nominal annual percentage rate (APR) compounded daily, or sometimes (and especially formerly) monthly, which in either case is not the same as the effective annual rate (EAR). Despite the "annual" in APR, it is not necessarily a direct reference for the interest rate paid on a stable balance over one year.
ஹி ஹி கடன் அட்டை வட்டி விதி!!!!!!!!!
நன்றி
நல்ல பயனுள்ள பதிவு.
ReplyDeleteமீண்டும் மீண்டும் படித்து புரிந்து கொள்ளப் பார்க்கிறேன்.
வாங்க சகோ தேவப்பிரியா,
Deleteஆமாம் அனைவரும் இந்த கணக்கு அறிவது பொருளாதாரம் சார் முடிவுகளுக்கு உதவும்.நன்றி!!
பல கடினமான கணிதக் கூறுகளை தமிழில் விளக்குவது நன்று. 15 ஆண்டுகளுக்கு கூட்டு வட்டி கணக்கிட நுண கணித முறையில் ஒரு எடுத்துக்காட்டு சொல்லுங்கள் நண்பரே.இதை லோக் பயன்படுத்தித்தான் கணக்கிட முடியும் அல்லவா?எக்ஸ்செல்லில் கணக்கிட முடியும் என்று நினைக்கிறேன்.
ReplyDeleteவாங்க சகோ முரளி,
Deleteஇப்பதிவின் நோக்கமே நுண்கணிதம், எல் ஹாஸ்பிடல் விதி நம் நடைமுறை வட்டிக் கணக்கீட்டிலும் உள்ளது என்பதைக் காட்டவே.எனினும் இது அறிவது அனைவருக்கும் நல்லதே.நாம் அதிகம் பயன்படுத்துவது எக்செல்.நீங்கள் கேட்ட அட்டவணை இட்டு விட்டோம்.
நன்றி!!!
Dear brother +infinity and -infinity is there but u said " many zero's and many infinity is there " i couldnd understant plz explain .
ReplyDelete
Deleteசகோ குரு வாங்க,
நாம் பல் அடிப்படை விடயங்கள் தெளிவாக வரையறுக்கப் பட்டதாக் நினைத்தாலும் அப்படி அல்ல. பாருங்கள் அடிப்படை அல்ஜீப்ராவின் படி பூச்சியம் என்பது மிக மிக குறைந்த அள்விட முடியாத நேர் எண்.
http://en.wikipedia.org/wiki/0_(number)
Elementary algebra
The number 0 is the smallest non-negative integer. The natural number following 0 is 1 and no natural number precedes 0. The number 0 may or may not be considered a natural number, but it is a whole number and hence a rational number and a real number (as well as an algebraic number and a complex number).
பாருங்கள் 0/0 என்பது சூழலுக்கு ஏற்ப பல மதிப்புகளைப் பெறுகிறது.
எ.கா
if x=0 sin(x)/x=0/0=1
if x=0 sin(2x)/x=0/0=2!!!
என்ன பொருள் பகுதியில் உள்ள பூச்சியம்,தொகுதியில் உள்ள பூச்சியமும் சமம் அல்ல என்பதுதானே!!!
http://gwydir.demon.co.uk/jo/numbers/interest/infinity.htm
இது முடிவிலிக்கும் பொருந்தும்.
பூச்சியம்,முடிவிலி இரண்டுமே வரையறுக்க முடியா விடயங்கள்!!
" அனைத்தையும் இழப்பதோ,அனைத்தையும் பெறுவதோ இயலா விடயம்"
நன்றி!!!
http://www.sciforums.com/showthread.php?55364-The-Value-of-nothing-is-everything
நல்ல பகிர்வு... வாழ்த்துக்கள்... நன்றி சார் (த.ம 101)
ReplyDeleteஇசெ சொன்னா மாதிரி கனடாகாரங்களுக்கு கிரெடிட் கார்ட் வட்டி பற்றி எழுதுவதோடு பைசாவட்டி, மூணு பைசா வட்டி, அஞ்சு பைசா வட்டி, பத்து பைசா வட்டி, மீட்டர் வட்டி, கந்து வட்டி, சுருள் வட்டி, டிஜிட்டல் வட்டி, டிஸ்கோ வட்டி, ராக்கெட் வட்டி, சாட்டிலைட் வட்டி குறித்துத்தெல்லாம் பதிவு எழுதினால் தமிழ் நாட்டு சனங்களும் மிகவும் குஷியாவோம்.
வாங்க சகோ நந்தவனத்தான்,
Deleteஇன்னும் எப்படி அடியாள்களை அனுப்பி வட்டி வசூல் செய்வதும் எழுதி விடுவோம். எதிர்பதிவாக எப்படி ஓடி ஒளிவது என்றும் எழுதுவோம். சரியா தலை!!
நன்றி!!!
த.ம. 1
ReplyDeleteவாங்க சகோ நம்பள்கி ,
Deleteத.ம 0/0
ஹி ஹி
நன்றி
நல்லது
ReplyDeleteவாங்க சகோ சௌந்தர்,
Deleteவருகைக்கும்,பின்னூட்டத்திற்கும் நன்றி!!
வணக்கம் சகோ.
ReplyDelete//அடுத்த பதிவு கணிதம் போட்டால் ஒருவரும் வரமாட்டார்.தனியா டீ ஆத்துவேன். பாவம் என்று சிலர் மட்டும் வந்து ஆறுதல் பின்னூட்டம் இடுவார்.//
அந்த பாவப்பட்ட ஆத்மாவில் நானும் ஒருத்தனா சகோ.?
நன்றி!!!!!!!!
இனியவன்...
வாங்க சகோ இனியவன்,
Deleteஹி ஹி புரிந்து விட்டதா!!
உங்களுக்கு விளக்கம் சொல்லியே ஓய்ந்து போயிட்டேன்!!
நன்றி
த.ம 102
ReplyDelete
Deleteசகோ குயிக் ஃபாக்ஸ் ,
நீங்கள் தினமும் 1001 அரபுக் கதைகள் வழங்குபவர் என்பதால்
த.ம 1001,1002.... னு அப்படிப் போகனும் சரியா!!
http://en.wikipedia.org/wiki/One_Thousand_and_One_Nights
One Thousand and One Nights (Arabic: كتاب ألف ليلة وليلة Kitāb alf laylah wa-laylah) is a collection of West and South Asian stories and folk tales compiled in Arabic during the Islamic Golden Age. It is often known in English as the Arabian Nights, from the first English language edition (1706), which rendered the title as The Arabian Nights' Entertainment.[1]
நன்றி!!
சகோ.சார்வாகன்,
ReplyDeleteநல்ல கணக்கீடு , நீங்க மிகவும் பிராபல்யப்பதிவர் ஆகிட்டிங்க போல எனவே கூட்டத்தை கட்டுப்படுத்த கண்ணீர்ப்புகை குண்டாக கணித குண்டு போட்டுவிட்டீர் என நினைக்கிறேன், ஆனாலும் வழக்கமாக வரும் ஆட்(டு)கள் வந்துக்கொண்டே இருக்கும் புதிய ஆடுகளே மந்தையை விட்டு தெறித்தோடும் என்பது புனித வேகாமத்தில் உள்ள "ஒரு மந்தையில் இருந்து பிரிந்த ஆடுகள் என்ற சொல்லாடலின் மூலம் அறியலம்.
கல்வெட்டு ஆதாரம் கேட்போர் மதுரை மேலூர் பி.ஆர்.பி கிரானைட்ஸ் குவாரிக்கு வருமாறு கேட்டுக்கொள்ளப்படுகிறார்கள்!!!
//வங்கி அளவுக்கும் வித்தியாசம் இருக்கும் ஏன் என்றால் பல வங்கிகள்
தொடர் கூட்டு வட்டி [Continuous Compound Rate] என்னும் முறையை பின்பற்றுகின்றன.//
நீங்கள் சொல்வது போல தான் என்றாலும் அடிப்படையில் வித்தியாசம் உண்டு, காலக்கணக்கீடு ஆண்டின் அடிப்படையில் தான் ஆனால் கொஞ்சம் வேறுபடும் எனக்கு தெரிந்ததை சொல்கிறேன்,
நிலை வட்டி விகிதம்,
மாறு வட்டி விகிதம்
என இரண்டு பயன்ப்படுத்துவார்கள், ரிசர்வ் பேன்க் அறிவிக்கும் ரெப்போ, ரிவர்ஸ் ரெப்போ போன்றவற்றின் அடிப்படையில் மாற்றிக்கொண்டே இருந்தால் ,மாறு வட்டி விகிதம் என்பார்கள்.
கடன் கால அளவு 10 ஆண்டுகள் , வட்டி விகிதம் 10% எனில்
முதல் ஆண்டுக்கு முழு கடன் மீது 10% வட்டியினை கணக்கிடுவார்கள், பின்னர் அடுத்த ஆண்டுக்கு ஒரு ஆன்டில் கட்டிய கடன் தொகையை கழித்துவிட்டு மூலதனத்தினை கணக்கிட்டு அதன் மீது 10% வட்டி என கணக்கிடுவார்கள். இப்படியே 10 ஆண்டுகளுக்கும் முன்னரே மொத்தமாக கணக்கிட்டு மூலதனம் + வட்டி கூட்டி அதனை மொத்த மாதங்களால் வகுத்து மாதத்தவணை கட்ட சொல்வார்கள்.
"continous compound rate of interest on dimnishing rate of principal" that is ccr interest on reducing balance", இப்படி ஏதோ புரியாத மாதிரி சொல்லுவாங்க வங்கியாளர்கள்.
நானும் பூதக்கண்ணாடி வச்சு அவங்க கொடுத்த பேப்பர்லாம் படிச்சு ஓரளவு புரிஞ்சுக்கிட்டாப்போல புரிஞ்சுக்கிட்டேன், அதை வைத்தே சொல்கிறேன் ,சரியான வங்கி வட்டிக்கணக்கீட்டினை யாராவது வங்கியாளர்கள் வந்து சொல்ல வேண்டும்.
சகோ வவ்வால்,
ReplyDeleteஅதாகப்பட்டது,
நீங்கள் எப்படி வட்டி கணக்கிட்டாலும் வங்கியின் கணக்கீட்டை விட குறைவாகவே இருக்கும்.
சட்டப்படி அவர்கள் ஆண்டுவீதம் மட்டும் சொன்னால் போதுமாம். எப்படி என சொல்ல தேவை இல்லையாம்.
சார்வாக பாகவதர்[பண்டாரம்??] பாடுகிறார்
பராசக்தி (1952)
எழுதியவர் : உடுமலை நாராயண கவி
தேசம் ஞானம் கல்வி ஈசன் பூசை யெல்லாம்
காசுமுன் செல்லாதடி - குதம்பாய்
காசு முன் செல்லாதடி.
ஈசனும் ஈசனார் பூசையும் தேசத்தில்
காசுக்குப் பின்னாலே - குதம்பாய்
காசுக்குப் பின்னாலே.
சாட்சியான பணம் கைவிட்டுப் போனபின்
சாட்சி கோர்ட்டு ஏறாதடி - குதம்பாய்
சாட்சி கோர்ட்டு ஏறாதடி.
பைபையாய் பொன் கொண்டோர்
பொய் பொய்யாய் சொன்னாலும்
மெய் மெய்யாய் போகுமடி - குதம்பாய்
மெய் மெய்யாய் போகுமடி.
நல்லவரானாலும் இல்லாதவரை
நாடு மதிக்காது - குதம்பாய்
நாடு மதிக்காது.
கல்வி இல்லாத மூடரை கற்றோர் கொண்டாடுதல்
வெள்ளிப் பணமடியே - குதம்பாய்
வெள்ளிப் பணமடியே
ஆரியக் கூத்தாடினாலும் தாண்டவக்கோனே - காசு
காரியத்தில் கண் வையடா தாண்டவக்கோனே
உள்ளே பகை வையடா தாண்டவக்கோனே
உதட்டில் உறவாடடா தாண்டவக்கோனே
முட்டாப் பயலையெல்லாம் தாண்டவக்கோனே - காசு
முதலாளி ஆக்குதடா தாண்டவக்கோனே
கட்டி அழும்போதும் தாண்டவக்கோனே - பிணத்தைக்
கட்டி அழும்போதும் தாண்டவக்கோனே - பணப்
பெட்டிமேலே கண் வையடா தாண்டவக்கோனே
நன்றி!!
சகோ சார்வாகன்,
ReplyDeleteகடனில் வாழ்க்கையை ஓட்டும் இந்த காலகட்டதிற்கு இந்த பதிவு சரியாக உதவும். ”பொட்டியை தட்டுபவர்களுக்கு” வட்டியை கணக்கீடு செய்ய நல்ல உத்தி.
இது எனக்கு பொருந்துமா என்று தெரியவில்லை. அனைத்து கடன்காரர்களும் கடன் தர அஞ்சுகிறார்கள். டிபிட் கார்ட்டே இல்லை என்றால் பார்த்துக்கொள்ளுங்கள்.
தற்போது புதிதாக வந்திருக்கும் ”சேட்டன்” வங்கிகளின் வட்டிதான் எனக்கு பரிச்சயமாக இருக்கிறது. இப்போது புரிகிறது ஏன் வட்டியை “தடை” செய்தார் என்று :)))).
////
ஆரியக் கூத்தாடினாலும் தாண்டவக்கோனே - காசு
காரியத்தில் கண் வையடா தாண்டவக்கோனே
////
பராசக்தி படத்தின் இந்த வரியை, தமிழ்நாட்டில் ஒருத்தரும் அவரும் குடும்பத்தாரும் நன்றாக புரிந்து பின்பற்றுகிறார்கள்.
நம்ம PCI சேர்மன் கட்ஜீ 1/0 indeterminate ஆ அல்லது முடிவிலியா என்ற சர்ச்சை பற்றி கொஞ்சம் எழுதுங்கள்.
நன்றி.
//டிபிட் கார்ட்டே இல்லை என்றால் பார்த்துக்கொள்ளுங்கள்//
Deleteநண்பர் நரேன், நான் விசாகாட்டிற்க்கு ஆசைபட்டு முதல்தடவையாக விண்ணபித்த போது எனது வங்கி உனக்கு தகுதியில்லை என்று மறுத்து விட்டது. இன்று வேறு நிறுவனம் ஒன்றே எனது பெயரில் விசாகாட் தயாரித்து அனுப்பி விசா காட்டை பெற்று கொண்டு விண்ணபத்தில் கையெழுத்திட்டு விண்ணபத்த மட்டும் திருப்பி அனப்பிவிடு என்று கேட்பதை என்ன சொல்வது. கடன் பட்டார் நெஞ்சம் போல,கடன் ஒரு தீயது, கார் வாங்குவதானா மட்டும் அல்லது வீடு வாங்குவதானா மட்டும் கடன் வங்கியில் பெற்று கொள் என்ற மிக நல்லநிலையில் இருக்கும் பெரியவங்க சொன்ன அறிவுரையை எனது வாழ்வின் மார்க்கமாக எனது வாழும் வாழ்க்கை வழி முறையாக ஏற்று கொண்டுள்ளேன்.
வாங்க சகோ நரேன்,
ReplyDeleteஉங்களுக்கு கடன் யாரும் தரவில்லை என்றால் உங்களுக்கு வருத்தம்,
கடன் கொடுத்தால் அவருக்கு வருத்தம்,
சீனா மார்க்க மேதை கன்ஃஃபுசியஸ் குழப்புகிறார் மன்னிக்கவும் விளக்குகிறார் பாருங்கள்!!
http://seeingwithc.org/jsblog/?p=1729
You ask credit.
I not give.
You get mad.
I give credit,
you not pay.
I get mad.
Better you get mad.”- Confucius
இதில் இருந்து எல்லா மார்க்க மேதைகளும் பண விடயத்தில் எச்சரிக்கை காட்டுவது அறிய முடியும்.
வட்டி தடை என்பதை பற்றி கேட்கிறீர்களா,
வட்டி என்பதை[ வழக்கம் போல்] வரையறையை மாற்றி விட்டால இது அனுமதிக்கப்படும்.
விளக்கம் சொல்லியே ஓய்ந்து விட்டேன்!!!
************
//பராசக்தி படத்தின் இந்த வரியை, தமிழ்நாட்டில் ஒருத்தரும் அவரும் குடும்பத்தாரும் நன்றாக புரிந்து பின்பற்றுகிறார்கள்.//
நிதி, நித்தி போன்றவை நீதியை விட வலியது!!!
ஆயினும் விதி வல்லியது!!!!!!!
//நம்ம PCI சேர்மன் கட்ஜீ 1/0 indeterminate ஆ அல்லது முடிவிலியா என்ற சர்ச்சை பற்றி கொஞ்சம் எழுதுங்கள்.//
நீதிபதிக்கு பல சமயம் நீதியே, நிதி கொடுத்தால் மட்டுமே கிடைக்கும் போது ,நிதி விதிகளையே மாற்றும் போது கணித விதி எம்மாத்திரம்?
1/0 = முடிவிலி,முடிவிலி...... முடிவிலி மட்டுமே!!!!!!!!1
நான் சரியாய்தான் சொல்கிறேனா?????!!!!!
http://www.thehindu.com/opinion/letters/article3855531.ece
In his article “Professor, teach thyself” (Sept. 3), Chairman of the Press Council of India, Markandey Katju, has cited an incident that took place when he was a judge of the Allahabad High Court. He says he chided a mathematics lecturer, whose case he was hearing, and told him that he was not fit to be even a teacher because he (the lecturer) said one divided by zero was infinity. Justice Katju claims that anything divided by zero is indeterminate. He is wrong and the lecturer was right because any non-zero number divided by zero is infinity. It is zero divided by zero that is indeterminate.
While I can understand the plight of the poor lecturer who did not have the courage to correct the judge hearing his case, I am appalled at the timidity of “some of the top senior academicians” of Jawaharlal Nehru University, to whom Justice Katju narrated the incident. I wonder why they let his fallacy pass unchallenged. Justice Katju must seek out the mathematics lecturer and apologise to him.
http://www.math.fsu.edu/~bellenot/class/f99/cal1/indeterminate.pdf
நன்றி.
சகோ,
ReplyDeleteseries of car bombs and mortar attacks in Iraq
Dozens of people have been killed in Iraq
என்பது அரபு இஸ்லாமிய ஈராக்கின் சாதாரண இஸ்லாமிய நடமுறை. அதை சொல்ல போனா என்னை அரபுக் கதைகள் வழங்குபவராக்கிவிட்டீர்களே.நன்றி
சகோ குயிகஃபாக்ஸ்
ReplyDelete1001 இரவுக் கதைகள் அல்லது அராபிய இரவுக் கதைகள் என்பது மிகவும் புகழ்பெற்ற கதைகள் ஒரு பெர்சிய தேச அரசன் தனது ஒரு மனைவி துரோகம் செய்ததால் பெண்களையே வெறுத்து,தினமும் காலையில் ஒரு பெண்ணை திருமணம் செய்து மறுநாள் காலையில் கொன்று விடுவான்.
இப்படி இருக்கும் அரசனிடம் ஒரு புத்திசாலிப் பெண் அரசனுக்கு இரவில் சஸ்பென்ஸ் கதைகள் சொல்லி கதை முடிவு அறிய அரசன் அவளை கொல்லாமல் விட்டு 1001 இரவுகள் தொடர்ந்து சொன்ன கதைதான் இது.
நீங்களும் அரபுலக கதைகளை தினமும் சொல்கிறீர்கள் அல்லவா?? அந்த ஒற்றுமையையே குறிப்பிட்ட்டேன்.
இக்கதைகளின் மூலம் அக்கால அரபு வாழ்வு,சூழல் ஆகியவை அறிய முடியும். நம் சகோக்கள் சொல்வது போல் புனித வாழ்வு இல்லாமல் ,நவரசமும்[சிருங்காரம் கொஞ்சம் அதிகம்] கொண்ட வாழ்வாகவே இருந்தது.
அபாசித்து வம்சத்தின் புகழ்பெற்ற அரசன் ஹாரூண் அல் ரஷீத்[ஆட்சி பொ.ஆ 763 to 809)] பல் கதைகளில் குறிப்பிடப்படுவார்.
அது பற்றிய தமிழ் விக்கி பிடியா படியுங்கள்!!
ஆங்கில புத்த்கம் தரவிற்க்கம் செய்யவும்!
தமிழ் இணைப்பு யாரேனும் சகோக்கள் தரலாம்
http://goo.gl/8A1Ju
download the book
http://www.wollamshram.ca/1001/Hardin/Hardin.pdf
வட்டி வாங்குறது ரொம்ப தப்பாமே ..! அதுனால இந்தப் பதிவை வாசிக்காமல் உட்டுட்டேன்.
ReplyDeleteவணக்கம் அய்யா வாங்க,
ReplyDeleteநீங்கள் அடைப்புக்குறி இல்லாமல் (தவறாக ) புரிகிறீர்கள்.
நீங்கள் மூல மொழியில் படிக்காததால் வரும் சிக்கலே இது!!!
வட்டி வாங்க கூடாது என்று புத்தகத்தில் இல்லை, ரிபா வாங்கக்கூடாது என்றுதானே இருக்கிறது.
ரிபா(Riba) என்பது அதிக, அநியாய வட்டி அவ்வளவுதான்
ஆகவே இப்படி பரியணும்.
வட்டி (அநியாயமாக,அதிகமாக) வாங்குறது ரொம்ப தப்பாமே ..!
விக்கிபிடியாவில் இருந்து
http://en.wikipedia.org/wiki/Islamic_banking
//Riba
The word "Riba" means excess, increase or addition, which according to Shariah terminology, implies any excess compensation without due consideration (consideration does not include time value of money). The definition of riba in classical Islamic jurisprudence was "surplus value without counterpart", or "to ensure equivalency in real value", and that "numerical value was immaterial."
Applying interest was acceptable under some circumstances. Currencies that were based on guarantees by a government to honor the stated value (i.e. fiat currency) or based on other materials such as paper or base metals were allowed to have interest applied to them.[10] When base metal currencies were first introduced in the Islamic world, the question of "paying a debt in a higher number of units of this fiat money being riba" was not relevant as the jurists only needed to be concerned with the real value of money (determined by weight only) rather than the numerical value. For example, it was acceptable for a loan of 1000 gold dinars to be paid back as 1050 dinars of equal aggregate weight (i.e., the value in terms of weight had to be same because all makes of coins did not carry exactly similar weight).//
வட்டி ( என்று பெயர் சொல்லாமல்,ஃப்ளாட் ரேட்டில்) வாங்கலாம்.
இது பற்றிய நம்ம பதிவு !!
இஸ்லாமிய வங்கி:வீட்டுக் கடன்: ஒரு சாமான்யனின் பார்வை/
http://saarvaakan.blogspot.com/2011/04/blog-post_25.html
நன்றி
சகோ.
ReplyDeleteநீதிமான் அப்படி இல்லை என்கிறாரே???
http://www.thehindu.com/opinion/letters/article3878423.ece
On infinity
In response to my article “Professor, teach thyself” published on September 3 in The Hindu, some persons have said that I was not correct when I wrote that anything divided by zero is an indeterminate number, not infinity. So let me prove what I said.
Suppose 1 divided by zero = x. Then x multiplied by 0 should be 1. But we know that anything multiplied by 0 becomes 0. It follows that it is impermissible to divide by 0.
Infinity is not a number at all. Infinity can be expressed thus: Limit of 1 divided by x, x tending to 0, is infinity. This merely means that if we keep making x smaller and smaller, the number keeps becoming bigger and bigger without any limit. That is all that infinity means. It is fallacious to regard it as a number.
Justice Markandey Katju,
நன்றி.
ReplyDeleteசகோ நரேன்,
நீதிபதி அய்யா சொலவதில் பாதி உண்மை
1.முடிவிலி என்பது வரையறுக்கப்படாத ஒன்று என்பதால் 1/0 என்பதும் வரையறுக்கபடாத ஒன்றே.
அதாவது முடிவிலி என்பதும் ஒரு எண் அல்ல. இதை நாமும் விவாதித்து இருக்கிறோம்.
ஆனால் 1/0 ம் ஒரு முடிவிலியே எனினும் முடிவிலி வரையறுக்கப் படாதது என்று ஏற்றால் மட்டுமே 1/0 வரையறுக்கப் படாதது.
1/0 என்பது முடிவிலி அல்ல என கூறவே முடியாது.
முடிவிலி வரையறுக்கப் படாதது என கூறுவதற்கும், 1/0 வரையறுக்கப் படாதது என கூறுவதற்கும் வித்தியாசம் உண்டு.முடிவிலி என்பது வரையறுக்க முடியா எண்ணற்ற எண்கள் கொண்ட குழு எண்கள்.1/0 ம் அதில் ஒரு உறுப்பினர்.
வேண்டுமானால் 1/0 என்பது வரையறுக்க முடியா முடிவிலி குழுமத்தை சேர்ந்த எண் என சொல்வது பொருந்தலாம்.
http://en.wikipedia.org/wiki/Division_by_zero
Thank you
அறிவியலில் எதற்கும்,அனைத்துக்கும் என்று கூறுவதைத் தவிர்த்தல் நலம். பெரும்பாலும் விதி விலக்கு இருக்கும். பூச்சியம் அல்லத ஒரு எண்ணை பூச்சியத்தல் வகுக்க கிடைப்பது முடிவிலி என்பதே வரையறை. முடிவிலி என்பது ஒரு எண் அல்ல, வரையறை செய்ய இயலாதது என்பது வேறு விடயம். நீதிபதி எந்த எண்ணும் பூச்சியத்தால் வகுபட்டால் என்னும் போதே அவரின் கூற்று குழப்பம் ஆகி விடுகிறது.
ReplyDelete1/0 = முடிவிலி என்பது கணிதத்தில் பயன்பாட்டில் எளிதில் பயன்படுத்தபடும் விடயம். முடிவிலி அள்விட முடியா விடயம் என்பது பயன்பாட்டை மாற்றுவது இல்லை.\
எப்படி 0/0 மற்றும் 1/0 மாறுபடுகிறது?
ஆனால் 0/0 0 முதல் முடிவிலி உடபட்ட எந்த மதிப்பையும் பெற இயலும். எ.கா
if x=0
x/(sinx)^2=0/0=infinity
x/sin(x)=1
sin(2x)/x=2
sin(mx)/x=m!!!!!!!!
1/0 முடிவிலிகளில் ஒன்று!!. ஒரு போதும் முடிவிலி அல்லாத மதிப்பை பெற இயலாது
தமிழர்களின் அறிவியல் தாய்மொழியான ஆங்கிலத்தில் கூறினால்
0/0=Indeterminate form
Indeterminate form
From Wikipedia, the free encyclopedia
In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution does not give enough information to determine the original limit, it is known as an indeterminate form.
1/0=infinity not indeterminate form but undefined
In mathematics, "infinity" is often treated as if it were a number (i.e., it counts or measures things: "an infinite number of terms") but it is not the same sort of number as the real numbers. In number systems incorporating infinitesimals, the reciprocal of an infinitesimal is an infinite number, i.e., a number greater than any real number. Georg Cantor formalized many ideas related to infinity and infinite sets during the late 19th and early 20th centuries. In the theory he developed, there are infinite sets of different sizes (called cardinalities).[2] For example, the set of integers is countably infinite, while the set of real numbers is uncountably infinite.
http://mathforum.org/dr.math/faq/faq.divideby0.html
0/0= in determinate
1/0 is undefined not indeterminate form
So Judge ayya is wrong!!!
சகோ.சார்வாகன்,
ReplyDeleteஜட்ஜுக்கு கெமிஸ்ட்ரி தான் ஒர்க் அவுட் ஆகும் ,கணிதம் ஆகாதாம் (கலா ,நமிதா ஆகிய அமர்வு நீதிபதிகள் சாட்சி)
முடிவிலி,வரையறுக்கப்படாதது இவை எல்லாம் கணிதத்தில் முடிவு தெரியாத விடைகளுக்கு போட்டு தப்பிக்க உதவும் தப்பிக்கும் வழியே.
எனவே நாம் ஏன் முடியை பிய்த்துக்கொள்ள வேண்டும் :-))
தெளிவாக தெரிந்தாலே சித்தாந்தம்
தெரியாமல் போனாலோ வேதாந்தம்...
காற்றுக்கு ஏது தோட்டக்காரன் போடி தங்கச்சி,
கள்ளிக்கு இருக்கு முள்ளில் வேலி இதான் என் கட்சி...
ஆதி எது அந்தம் எது...
ல லா லல்லா லா ,,ஆ ஆ ஆ,,,!!!
கூகுள் தந்த வீடு பிளாக்கு இருக்கு..
ReplyDeleteஇதில் நீ என்ன ,நான் என்ன
போட்டப்பதிவு என்ன ...வந்த பின்னூட்டம் என்ன
ஞான சார்வாகரே...
ஹி...ஹி பாட்டில் பல்லவி சேர்க்காமல் போயிட்டேன் .