சமரசம் உலாவும் இடமே!!!!: கணித சம‌ன்பாடுகளின்[mathematical equations] வகைகள்

Monday, October 17, 2011

கணித சம‌ன்பாடுகளின்[mathematical equations] வகைகள்

அறிவியலில் கணிதம் என்பது பிரிக்க முடியாத அங்கம் என்பதை அனைவருமே ஒத்துக் கொள்வோம்.இயற்கையின் நிகழ்வுகளை விளக்குவதே அறிவியல்.அந்நிகழ்வுகளின் காரணிகளை(parameters) வரையறுத்து அக்காரணிகளின் இடையே உள்ள தொடர்பை சமன்பாடுகள் மூலமாக வரையறுப்பதே இதன் பரிணாம வளர்ச்சி.

எ.கா

நுயுட்டனின் ஈர்ப்பு விதி(Newton’s law of gravitation) பற்றிய சமன்பாடு. இரு பொருள்களுக்கிடையே ஏற்படும் ஈர்ப்பு விசை அவ்ற்றின் எடைகளின் பெருக்கத்திற்கு(m1*m2) நேர் விகிதத்திலும்,அதன் தூரத்தின் இருமடிக்கு(r^2) எதிர்விகிதத்திலும் இருக்கும் என்பதே விதி ஆகும்.இதனை கணித சமன்பாடாக கீழ்க்கண்ட முறையில் எழுத முடியும்.

$F = G \frac{m_1 m_2}{r^2}\$

Diagram of two masses attracting one another

where:

· F is the force between the masses,

· G is the gravitational constant,

· m₁ is the first mass,

· m₂ is the second mass, and

· r is the distance between the masses.

பிறகு மாறிலி Gன் மதிப்பை பல சோதனைகள் மூலம் கண்டறிய முடியும் [G=6.674×10⁻¹¹ N m² kg⁻²]

இப்பதிவில் பொதுவாக கணித சம்ன்பாடுகள் வகைகள்,அவற்றின் பயன் பாடுகள் பற்றி கூறுவது மட்டுமே நோக்கம் .

மே கூறிய சமன்பாடு மூன்று காரணிகளை கொண்டது

1.முதல் பொருளின் எடை(m1)

2.இரண்டாம் பொருளின் எடை(m2)

3. இரு பொருள்களின் (ஈர்ப்பு மையங்களுக்கிடையே) இடையே உள்ள தூர‌ம்(r)

பொதுவாக கணித சமன்பாடுகளை இரு வகையாக பிரிக்கலாம்.

1.அல்ஜீப்ரா சமன்பாடுகள். [Algebraic equations]

2. வகைகெழு சமன்பாடுகள். [Differential equations]

இன்னும் discrete equations என்று ஒரு வகை உண்டு என்றாலும் அது தொடர்சியான சமன்பாடுகளில்(continuous domain equations) வராது.

மேலே கண்ட சமன் பாடு ஒரு அல்ஜீப்ரா சமன்பாடு ஆகும்.எப்படி என்று கேட்கிறீர்களா ?. அல்ஜீப்ரா சமன்பாடு என்பது ஒரு சமன்பாட்டில் உள்ள அனைத்து காரணிகளும் நேரம்(time) அல்லது எதனை பொறுத்தும் மாறாமல் இருந்தால் அது அல்ஜீப்ரா சமன்பாடு ஆகும்.

அதாவது ஒரு குறிப்பிட்ட தூரத்தில் உள்ள குறிப்பிட்ட அளவு எடைகளுக்கு இடையே உள்ள விசையின் அளவை இந்த சமன்பாடு கணக்கிடுகிறது.

http://en.wikipedia.org/wiki/Newton's_law_of_universal_gravitation

இப்போது இரண்டாவது பொருள் ஒரு அலகு(unit) எடை கொண்டதாக் வைத்துக் கொள்வோம்.அது முதல் பொருளில் இருந்து நகர்ந்து செல்வதாக் கொண்டால் அச்சமன்பாட்டில் தூரம் என்பது மாறக் கூடியதாக் உள்ளதால் இதனை வகை கெழு சமன்பாட்டின் மூலமே கூற இயலும்.

The differential form of Gauss's law for gravity states: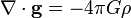

$\nabla\cdot \mathbf{g} = -4\pi G\rho$

Where

$\nabla\cdot$ Denotes divergence, [வகைகெழுவில் மூன்று(gradient,divergent,curl) வித பயன் பாடுகள் உண்டு.இது பற்றி தனி பதிவிடுகிறேன்].

g=gravitational intensity

G is the gravitational constant of the universe,

ρ is the mass density at each point.

கணித அறிஞர் காஸ்(Gauss 1777_1855 CE) ன் ஈர்ப்பு விசைக்கான வகை கெழு சமன்பாடு கீழே கொடுக்கப் படுகின்றது. இச்சமன்பாட்டை நியுட்டனைன் அல்ஜீப்ரா சமன்பாடாக மாற்ற இயலும்.

ஆகவே சமன்பாட்டில் உள்ள காரணிகள் (பொதுவாக) நேரம் பொறுத்து மாறும் போது அதற்கு வகை கெழு சமன்பாடு பயன் படுத்துகிறோம்.அல்ஜீப்ரா சமன்பாட்டை வகைக்கெழு சமன்பாடாக எளிதில் மாற்றலாம்.அனைத்து வகை கெழு சமன்பாடுகளையும் அல்ஜீப்ரா சமன்பாடாக தீர்வு காண்பது கடினம்.சில தோராய தீர்வுகளே சில சமயங்களில் பயன் படுத்தப் படுகின்றன.

ஆகவே இப்பதிவின் மூலம் சொல்வது என்ன?

1.சமன்பாடுகள் என்பது ஒரு இயற்கை(செயற்கை) நிகழ்வின் காரணிகளுக்கு இடையே உள்ள தொடர்பு ஆகும்.

2.காரணிகள் அக்குறிப்பிட்ட சூழலில் மாறாமல் இருக்கும் போது அவை அல்ஜீப்ரா சமன்பாட்டின் மூலம் தொடர்பு படுத்தப் படுகின்றது.

3.ஒன்று அல்லது அதற்கு மேற்பட்ட காரணிகள் காலம் பொறுத்து மாறும் போது வகைக்கெழு சமன்பாடாக தொடர்பு படுத்தப் படுகின்றது.

4.அல்ஜீப்ரா சமன்பாடு வகைகெழு சம்ன்பாடாக (எளிதில்) மாற்ற இயலும்.அனைத்து வகை கெழு சமன்பாடுகளையும் அல்ஜீப்ரா சமன்பாடாக மாற்ற இயலாது.

எ.கா வில் சொன்ன சமன் பாடு புரியவில்லை எனில் Be cool!!!!!!!. வகைகெழு சமன்பாடுகள் அதன் வகைகள் பற்றி ஒரு பதிவிடுவேன். இது குறித்த உங்கள் சந்தேகங்களுக்கு விளக்க்ம் அளிக்க தயாராக உள்ளேன்,

ஒரு புதிர் சகோ இரப்பானி அளித்தார் அதையும் இங்கே இணைத்து விடுகிறேன்!‌

/ஒரு விவசாயி 100 ரூபாய் வைத்துள்ளார் , பழக்கடைக்கு செல்கிறார் கடையில் மா,பலா,வாழை என்ற 3 வகை பழங்கள் மட்டும் உள்ளது அதன் விலை மா ஒன்று=75 பைசா பலா ஒன்று = 5 ரூபாய் வாழை ஒன்று = 25 பைசா என்று வைத்துக்கொண்டால் ( விலையில் எந்த மாற்றமும் இல்லை) விவசாயிடம் உள்ள 100 ரூபாயிக்கு 100 பழம் வாங்கவேண்டுமெனில் எத்தனை மா,பலா,வாழை ???? இதற்க்கு விடை தெரிந்தால் சொல்லவும்/

ஸ்லாம் சகோ ர‌ப்பானி

இதனை இரு சமன்பாடுகளாக வடிவமைக்க்லாம் ஆனால் 3 மாறிகள்.ஆக எண்ணற்ற தீர்வுகள் இருக்க்லாம்.ஆனாலும் பழங்களை முழுமையாக வாங்குவதாகவே கணக்கிட வேண்டும் ஆகவே தீர்வு முழு எண்கள்(integer) மட்டுமே.என்னால் 5 தீர்வுகள் வரை கண்டறிய முடிந்தது.புதிருக்கு நன்றி

0.75x+5y+0.25z=100

x+y+z=100

X,y,z=integers

தீர்வுகள்	z வாழை 0.25	y பலா 5	x மா 0.75
1	1	6	93	100
2	18	8	74	100
3	35	10	55	100
4	52	12	36	100
5	69	14	17	100

நன்றி சகோ இரப்பானி

24 comments:

ramalingamOctober 17, 2011 at 10:39 AM
நல்ல முயற்சி. தொடருங்கள்.
ReplyDelete
Replies
சார்வாகன்October 17, 2011 at 11:07 AM
நன்றி ramalingam
ReplyDelete
Replies
நிரூபன்October 17, 2011 at 1:44 PM
வணக்கம் பாஸ்,

கணிதத்தை மென்மையான தமிழ் கலந்து அருமையான விளக்கப் பதிவாகத் தந்திருக்கிறீங்க.
ReplyDelete
Replies
RabbaniOctober 17, 2011 at 4:37 PM
ஸலாம் சகோ சார்வாகன்
சமன்பாடுகள் பற்றி பதிவு???????இதில் சந்தேகம் ஒன்றும் இல்லை ஆனால் 3 கிளாஸ் கணக்குத்தான் தீர்வு தெரியல
அந்த 3 கிளாஸ் கணக்கு இதோ உங்களது பார்வைக்கு

ஒரு விவசாயி 100 ரூபாய் வைத்துள்ளார் , பழக்கடைக்கு செல்கிறார் கடையில் மா,பலா,வாழை என்ற 3 வகை பழங்கள் மட்டும் உள்ளது அதன் விலை மா ஒன்று=75 பைசா பலா ஒன்று = 5 ரூபாய் வாழை ஒன்று = 25 பைசா என்று வைத்துக்கொண்டால் ( விலையில் எந்த மாற்றமும் இல்லை) விவசாயிடம் உள்ள 100 ரூபாயிக்கு 100 பழம் வாங்கவேண்டுமெனில் எத்தனை மா,பலா,வாழை ???? இதற்க்கு விடை தெரிந்தால் சொல்லவும்
ReplyDelete
Replies
சார்வாகன்October 17, 2011 at 5:42 PM
நன்றி நண்பர் நிரூபன்
ReplyDelete
Replies
சார்வாகன்October 17, 2011 at 5:48 PM
நன்றி சகோ இரப்பானி
அதையும் பதிவில் இணைத்து விடுகிறேன்
நன்றி சகோ இரப்பானி
ReplyDelete
Replies
narenOctober 17, 2011 at 7:56 PM
நல்லப் பதிவு, அல்ஜிப்பரா சுலபமாக புரிந்துக்கொள்ள முடிகிறது. ஆனால் இந்த differential equations.ம்ம்ம்ம்ம் புலப்படாதது. அடிப்படையே இப்படி என்றால், இதில் ph.d செய்பவர்கள் எல்லாம் என்ன படிப்பார்களோ??

பதிவுக்கு நன்றி, differential equations அறிமுகப்படுத்தியதிற்கு நன்றி.
ReplyDelete
Replies
சார்வாகன்October 17, 2011 at 8:17 PM
வாங்க நரென்
இந்த differential equations என்பதை புரிய வேண்டுமெனில் மாற்றம் ஒன்றே மாற்றம் இல்லாதது என்பதை ஞாபகம் வைத்துக் கொண்டால் போதும்.ஒவ்வொரு மாறியின்(variable) மாற்றத்தையும்(rate of change) சமன்பாடாக்குவதே differential equations .இது பற்றி இன்னும் சில பதிவுகள் இடுலாம்.

நன்றி
ReplyDelete
Replies
narenOctober 17, 2011 at 9:01 PM
நமக்கு கடினம், புரியாதது, முடியாதது என்பவைகள் எல்லாம், சுலபம், புரியும், முடியும் என்பது வரை பிடிக்கும்.
அதனால் இடுக்கை ஈடுங்கள், லிங்குகள், ஒரு கைப் பார்ப்போம்.
நன்றி.
ReplyDelete
Replies
RabbaniOctober 17, 2011 at 9:45 PM
ஸலாம் சகோ சார்வாகன்
அந்த பழங்கள் புதிருக்கு 5 answer தந்து அசத்திபூட்டீர்கள் எனக்கு
69 X 0.25+17X0.75+14X5 என்ற தீர்வு மட்டும் தெரியும்
பதிவில் இணைத்தமைக்கு நன்றி
இந்த புதிருக்கு தீர்வு தெரிந்தால் சொல்லவும்

நான்கு குகை வருசையாக இருப்பதாக வைத்துகொள்வோம் ஒவ்வொரு குகை யும் ஒரு நுழை வாயில் , ஒரு வெளியேறும் வழி உள்ளது இங்கு ஒரு குறிப்பிட்ட தொகை கட்டணமாக செலுத்தவேண்டும் அது எவ்வளவு என்றாலும் இருக்கலாம் ஆனால் சமமாக இருக்கவேண்டும் மேலும் ஒவ்வொரு குகை யின் நடுவில் ஒரு recharge point உள்ளது இங்கு அந்த சமயம் எவ்வளவு தொகை உள்ளதோ அது போல் ஒரு மடங்கு உங்களுக்கு கிடைக்கும் அதாவது உங்களிடம் recharge பாயிண்ட் யை அடையும் போது 2 Rs இருந்தால் இன்னும் ஒரு 2 Rs கிடைத்து 4 Rs ஆகும் ஆரம்பத்தில் எவ்வளவு தொகை வேண்டும் என்றாலும் எடுத்துக்கொள்ளலாம். இவ்வாறு இந்த விதிகளுக்கு உட்பட்டு தொடர்ச்சியாக நான்கு குகை களையும் கடந்து இறுதியில் வெளியேறும் போது எந்த வித தொகையும் இன்றி வர வேண்டும் அதாவது கடைசியில் (௦௦0) தொகை யுடன் வரவேண்டும்

குறிப்பு : ஒரு குகை விட்டு மறு குகை செல்லும்போது எவ்வித தொகையும் சேர்க்க , கழிக்க கூடாது மேலும் நான்கு குகையில் முறையே நான்கு நுழைவாயில் , நான்கு வெளியேறும் வழி உள்ளது இங்கு செலுத்தும் தொகை சமமாக இருக்கவேண்டும்.

கேள்விகள்
1 entrance fee ?
2 எவ்வளவு தொகை எடுத்துச்செல்லவேண்டும்?
ReplyDelete
Replies
சார்வாகன்October 18, 2011 at 5:21 AM
ஸ்லாம் சகோ.
நீங்கள் கேட்ட புதிரின் தீர்வு
X=initial money
Y=charge
When crossed the first cave 2*(x-y)
When crossed the second cave 2(2x-3y)=4x-6y
When crossed the third cave 2(4x-6y-y)=8x-14y
When crossed the fourth cave 8x-15y=0
Lets us assume y=1 then x=15/8=1.875

When crossed the first cave 2*(1.875-1)=1.75
When crossed the second cave 2*(1.75-1)=1.5
When crossed the third cave 2(1.5-1)=1
When crossed the fourth cave 1-1=0

It has infinite solutions .If you want to make x as an integer y=8 then x=15
When crossed the first cave 2*(15-8)=14
When crossed the second cave 2*(14-8)=12
When crossed the third cave 2(12-8)=8
When crossed the fourth cave 8-8=0

மன்னிக்கவும் தமிழில் தட்டச்சு செய்ய நேரம் இல்லை.எக்செல்(excel) ஷீட்டில் பல புதிர்களுக்கு விடைகாண இயலும்.அது பற்றியும் ஒரு இடுகை இட முயற்சிக்கிறேன்.அதவது வார்த்தையில் உள்ளதை சமன்பாடாக மாற்றி விட்டால் தீர்வு எளிது.நன்றி
ReplyDelete
Replies
RabbaniOctober 19, 2011 at 12:06 PM
mr saarvaakan
Please read the puzzle once again
in first cave there are two counter such as entry and exist we should pay entry and exist fees. The center of cave has recharge point
as per your answer
x=1.875 and y=1
first cave entry fee 1 when we reaching recharge point-1 (center of first cave) we gain 0.875, so we have 1.75. after that we need to pass the first cave's exist & second cave's entry so 1.75 not enough to pay first cave exist fee (1)and second cave entry fee (1).
ReplyDelete
Replies
சார்வாகன்October 19, 2011 at 1:52 PM
Dear Mr rabbani i have explained the modell and solving for one time fee.You can do it for any type.
மீன் பிடிக்க கற்றுக் கொடுக்க மட்டுமே விரும்புகிறேன்.மீன் பிடித்து தர அல்ல.நீங்கள் சொன்ன இரு வாசல்களிலும் கட்டணம்(எந்த ஊரில் இப்படி?)இதற்கும் சமன்பாடு அமைத்து விட்டேன் நீங்கள் இது போல் சமன்பாடு அமைத்தால் சரி தவறு சொல்கிறேன்.முயற்சிக்கவும்
நன்றி
ReplyDelete
Replies
சார்வாகன்October 19, 2011 at 2:03 PM
only answer X=2.8125 y=1 i want equation
ReplyDelete
Replies
RabbaniOctober 19, 2011 at 4:16 PM
ஸலாம் சகோ சார்வாகன்
கணிதத்தில் உங்களுக்கு இருக்கும் அனுபவத்தை உணர்ந்து கொள்ளமுடிந்தது உங்களது விடை சரியாக உள்ளது இதற்க்கு என்ன சமன் பாடு என்று வினவியுள்ளீர்கள் இதோ நான் முயற்சிக்கிறேன்

capital amount=X
enterance or exist fee=Y

@ center of first cave
2(x-y)

@ center of second cave
2(2x-4y)
@ center of third cave
2(4x-10y)
@ center of fourth cave
2(8x-22y)

finally
the equation
16x-45y=0
if y=1
x=45/16
x=2.8125
நீங்கள் எதிர்பார்த்ததை தந்துவிட்டேன் எனநினைக்கிறேன்
ReplyDelete
Replies
சார்வாகன்October 19, 2011 at 4:24 PM
நன்று சகோ இரப்பானி
இப்போது 4 குகைகள் மட்டும் உள்ளதால் இந்த சமன்பாடு(16x-45y) வருகிறது.இப்படியே 100,200 என்று போய்க் கொண்டே இருந்தால் எப்படி சமன்பாடு அமைப்பது அதாவது "n" குகைகளுக்கு பிறகு இறுதி பணம் சூன்யம் எனில் தீர்வு எப்படி variable இருக்கும் என யோசியுங்கள்.

முயற்சிக்கவும் இல்லையெனின் தருகிறேன்.
நன்றி
ReplyDelete
Replies
RabbaniOctober 19, 2011 at 4:39 PM
"நீங்கள் சொன்ன இரு வாசல்களிலும் கட்டணம்(எந்த ஊரில் இப்படி?)"

நான் ஓமன் இல் வசிக்கிறேன் இங்கிருந்து சாலை வழியாக UAE நுழையும் போது UAE அரசு விசா கட்டணம் 100 திர்ஹம் வசூலிக்கிறார்கள் பயணம் முடிந்து UAE விட்டு வெளி ஏறும் போது exist fee 30 திர்ஹம் வசூலிக்கிறார்கள்
ReplyDelete
Replies
சார்வாகன்October 19, 2011 at 4:45 PM
வாங்க சகோ இரப்பானி பகல் கொள்ளையாக இருக்கிறதே!.சம்பாதிப்பது இப்ப்டியே கொடுக்க வேண்டியதுதான்!
ReplyDelete
Replies
RabbaniOctober 19, 2011 at 5:33 PM
please you give equation for n cave
ReplyDelete
Replies
TamilanOctober 19, 2011 at 8:07 PM
அந்த நீல,பச்சை கலர் உருண்டை பார்பதற்கு அழகாக இருக்கிறது.
ReplyDelete
Replies
சார்வாகன்October 19, 2011 at 8:08 PM
Dear bro rabbani
This the equation u have asked
(2^n)* x-3((2^n)-1)*y=0
n=குகை எண்ணிக்கை
if n=4 you get (2^4)*x-3((2^4)-1)*y=0
16x-45y=0
if n=10
1024x-3069y=0
I appreciate your interest .I enjoyed it. Thank you
ReplyDelete
Replies
சார்வாகன்October 19, 2011 at 8:10 PM
வாங்க தமிழன் நலமா!
நன்றி
ReplyDelete
Replies
TamilanOctober 19, 2011 at 8:11 PM
நலமே. நீங்கள் எப்படி?
ReplyDelete
Replies
TamilanOctober 19, 2011 at 8:14 PM
எனக்கும் கணக்குக்கும் கொஞ்சம் தூரம் அதிகம் . நீங்கள் குடுத்திருப்பதை புரியும் வரை படித்துவிட்டு திரும்பவும் வரேன்.
ReplyDelete
Replies

Add comment

சமரசம் உலாவும் இடமே!!!!

Monday, October 17, 2011

கணித சம‌ன்பாடுகளின்[mathematical equations] வகைகள்

24 comments:

Earth Clock

visitors