வணக்கம் நண்பர்களே!
சென்ற பதிவில் கற்றது இதுதான்.ஒரே ஒரு வரையறுப்பு
"தொகை நுண்கணிதம் என்பது ஒரு மாறித்
தொடர்பு, அதன்
எல்லைகளால் அடைபடும் பரப்பள்வு கணிப்பது ஆகும்"
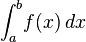 (1)
(1)
Integral is defined
informally to be the area of the region in the xy-plane bounded by the graph of f, the x-axis, and the vertical lines x = a and x = b, such that areas above the axis add to the total,
and the area below the x axis subtract from the total.
இதனை கொஞ்சம் விளங்குவோம்!
இந்த தொகைக் கெழு[integral] என்பதிலும் பலவகை உண்டு நாம் பார்த்தது ஒரு அடிப்படை
விடயமே.. இது இரு பரிமாண தளத்தில்
எல்லைகளுக்கு உட்பட்ட பரப்பளவாக வரையறுக்க ப்படுகிறது.
"தொகைக்கெழு என்றால் இருபரிமாண தளத்தில்
எல்லைகளுக்குள் உட்பட்ட பரப்பு"
அது என்ன எல்லைகள்?
நாம் எப்போதும் சொல்வது ஒரு சரியான கேள்வியில் பாதி பதில்
ஒளிந்து கொண்டு இருக்கும்.கேள்வியில் உள்ள
தொழில் நுட்ப சொற்களின் வரையறுப்பை சரியாக அறிவதுதான் அந்த பாதி பதில்.
பரப்பு என்பது ஒரு இரு பரிமாண அள்வு.பரிமாணங்கள் ஒவ்வொன்றும்
ஒன்றுக்கொன்று செங்குத்தாக இருக்க வேண்டும்(ஏன்?).
அப்போது பரப்பு என்பது செங்குத்தான எல்லைகளால் சுற்றி
வளைக்கப்படும் அலகு ஆகும்.ஒரு சதுரம் என்பதே அடிப்படை அலகு.இதற்கு நான்கு பக்கங்கள்
உண்டு. ஆகவே தொகைக்கெழுவின் எல்லைகள் நான்கு .
எளிமையாக இப்படியும் கூறலாம்.
ஒரு இருபரிமாண தளத்தில் இரு அடிப்படை அச்சுகளை கொண்டு
வரையப்படும் மூடப்பட்ட அமைப்பு சதுரம் (அல்லது செவ்வகம்) ஆகும்
எல்லை எப்படி இருக்க வேண்டும்?
இருபரிமாண தளத்தில் அடிப்படை அச்சுகளை கொண்ட செவ்வகம்
குறிக்க நான்கு எல்லைகள் தேவை.
X அச்சில் இரண்டு அளவும், Y அச்சில் இரண்டு அளவும் இருக்க வேண்டும்.
தொகைக்கெழு என்பது ஒரு மாறித்தொடர்பின் மீது செய்யப்படும்
ஒரு செயலாகும். மாறித்தொடர்பு[function] என்பது ஒரு
சார்ந்த மாறி[dependent variable] சார்பற்ற மாறியின்[independent variable] தொடர்பாக வரை யறுக்கப்படுகிறது.
1y=f(x)
X அச்சின் அள்வுகள் என்ன
1.) x=a
2),x=b
Y அச்சின் அள்வுகள் என்ன?
3)y=0
4)y=f(x)
என்ன சகோ முதல் மூன்று எல்லைகளும் அண்டை பக்கத்திற்கு செங்குத்தானவை. ஆனால் y=f(x) என்ற எல்லை வளைகோடு அலலவா
என்றால் ஒன்று மட்டும் அப்படி இருக்கலாம்(ஏன்?). ஆனால் மொத்தம் நான்கு பக்கம் மட்டுமே பரப்புக்கு இருக்க வேண்டும்.
தொகைக்கெழு காண்பதற்கு பிரதியிடுதல் முறை[substitution method],பகுதி முறை[by parts] என இரு வகைகள் உண்டு.அது
எல்லாம் சூத்திரம் என்று பள்ளிப்பாடம் போல் செல்லும். நாம் எப்படி எளிய முறையில் தொகைக்கெழு
என்பதை புரிதலிலேயே கவனம் செலுத்துகிறோமே தவிர,சூத்திரம் மனப்பாடம் செய்து புதிர்களை
தீர்ப்பது குறித்து அல்ல.
இப்போது இருபரிமாணத்தில் தொகைக்கெழு புரிந்து இருக்கும்.சரி
முப்பரிமாணத்தில் எப்படி என்றால அதையும் பார்ப்போம்.எனினும் இபோதும் இருபரிமாண தளத்திலேயே
தொகைக்கெழுவின் சில பயன்பாடுகள் பற்றி அறிவோம். அனைத்து தொகைக்கெழுவையும் மேலே கூறிய
இருமுறைகள்,சூத்திர உதவியுடன் தீர்க்க இயலாது.அப்போது தோராயமாக NUMERICAL INTEGRATION முறையில் தீர்க்க வேண்டும்
இதனையும் நாம் கற்போம்.தொகைகெழு என்றால் பரபளவு என்று கூறினோம்.இதற்கு நிரூபணம் உண்டா?
இத்னை NUMERICAL INTEGRATION பார்க்கும் போது விளக்கினால் போயிற்று.
&&&&&&&&&&
ஒரு வளைகோட்டின்[curve] நீளம் எப்படி தொகைகெழு மூலம் கண்க்கிடுவது என்பதை கற்போம்.
ஒரு வளை கோட்டின் கீழ் அச்சுகளினால் அடைபட்ட பரப்பளவுதான்
தொகைக்கெழு என அறிந்தோம்.இபோது ஒரு வளை கோட்டின் நீளம் அறிவது எப்படி என அறிவோம்.
ஒரு இருபரிமாண தளத்தில் மாறித்தொடர்பு வளை கோடாக குறிக்கப்படுகிறது.நேர்
மாறி சம்ன்பாடுகள் கோடுகளாகும்.நாம் வளை கோடு பற்றி மட்டும் கவனம் செலுத்துவோம்.
ஒவ்வொரு செயல்முறைக்கும் ஒரு எளிய அடிப்படை விதி இருக்கும்.
வளைகோட்டீன் நீளத்திற்கும் அது பொருந்தும்.
வளை கோடு என்றால் என்ன?
வளைந்து செல்லும் கோடே வளை கோடு என்றா சொல்வோம்???????..தவறு.வளை கோடு என்பது மாறித்தொடர்பின்
குறியீடு. X ன் ஒவ்வொரு மதிப்புக்கும் Y[i.e f(x)]என்ன மதிப்பு பெறுகிறது என்பதை
கணக்கிட்டே வளைகோடு வரைகிறோம்.
[x1,y1],[x2,y2],[x3,y3]……[xN,yN]
இப்போது இடைவெளிகள்
மிகச்சிறியது என் வைத்தால் மட்டுமே வளைகோடு மிக சரியாக வரும். அப்படி மிக குறைந்த இடைவெளியில்[almost zero] அப்புள்ளிகளுக்கு உள்ள பாதை
நேர் கோடாகவே இருக்கும்.
இது எப்படி?
இரு புள்ளிகளுக்கு இடையே உள்ள மிக குறைந்த தூரமே நேர்
கோடு!. என்பதே நேர்கோட்டின் இலக்கணம் ஆகும்.
இப்போது வளைகோடின் மீது மிக அருகில் உள்ள இரு புள்ளிகலை
எடுத்துக் கொள்வொம். அவற்றின் ஆயத் தொலைகள்
(x1,y1) and (x2,y2)
இந்த இருபுள்ளிகளுக்கு இடையே உள்ள தூரம் என்ன?
ஆயத்தொலைகளின் வர்க்கங்களின் கூட்டுத்தொகையின் வர்க்கமூலமே
இருபுள்ளிகளின் தூரம் ஆகும்.சூத்திரமாக கூறினால்.



dx=x2-x1
dy=y2-y1
dy=y2-y1
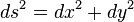

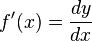
![s = \int_{a}^{b} \sqrt { 1 + [f'(x)]^2 }\, dx.](http://upload.wikimedia.org/wikipedia/en/math/e/1/d/e1daf29d3659657638edc2a0f89ad941.png) (2)
(2)ஆகவே ஒரு வளை கோட்டின் நீளம் அறியவேண்டும் எனில் அதன் சிறுமாற்ற விகித வர்க்கத்துடன் ஒன்றை சேர்த்த வர்க்க மூலத்தின் தொகைக்கெழு ஆகும்.
http://en.wikipedia.org/wiki/Arc_length
இதேபோல் ஒரு வளைகோட்டின் பரப்பு X அச்சினை சுற்றினால வரும் கன அள்வின் சூத்திரம்
 (3)
(3)


இந்த சூத்திரம் எப்படி வந்தது எனில் வளை கோட்டின் கீழ் உள்ள பரப்பு அச்சினை சுற்றும் போது பல வட்டங்களை ஏற்படுத்துகிறது.

வட்டத்தின் ஆரம் .f(x) ஆகவே மொத்த வட்டங்களின் கூட்டுவதற்கு தொகைக்கெழு x ஐ பொறுத்து காணவேண்டும்[ஏன்?].
நண்பர்கள் இதே போல் பரப்பளவின் சூத்திரத்திற்கும் விள்க்கம் அளிக்க முயற்சிக்கலாமே!!!!!நாம் சூத்திரம் மன்ப்பாடம் செய்ய அல்ல சூத்திரம் வடிவமைக்கும் விதத்தையே கற்க,கற்பிக்க விரும்புகிறோம்.
அடுத்த பதிவில் numerical integration பற்றிப் பார்ப்போம்.முப்பரிமாணத்தில் தொகைக்கெழுவின் பயன்பாடுகளையும் பார்ப்போம்.
இதுவரை கற்றது.
1. மாறித்தொடர்பின் எல்லைககுட்பட்ட தொகைகெழு பரப்பளவு.
2. மாறித்தொடர்பின் சிறுமாற்ற விகிதத்தின் வர்க்கத்துடன் ஒன்றை கூட்டிய வர்க்க மூலத்தின் எல்லைககுட்பட்ட தொகைகெழு வளைகோட்டின் நீளம்.
3. மாறித்தொடர்பின் வர்க்கத்தின் 'pi' மடங்கின் எல்லைககுட்பட்ட தொகைகெழு கன் அள்வு.
சமன்பாடுகெளே இல்லாமல் எளிய தமிழில் கணிதம் விளக்கும் ஒரு முயற்சி.மேம்படுத்தும் கருத்துகளை வணக்கத்துடன் வரவேற்கிறோம்.
நன்றி
(தொடரும்)
நண்பரே அடிப்படை நன்றாக புரிந்தது,
ReplyDeleteஅதிகமாக theoretical ஆக இருப்பதால் கொஞ்சம் பிடிப்படுவது கடினம்தான். இத்ன் practical applications நடைமுறை செயலாக்கங்களை வைத்து விளக்கினால் இன்னும் எளிமையாக இருக்கும்.
பெத்த பெத்த பல்கலைகழகங்களில் இதைப்பற்றி இப்படிதான் பாடங்கள் எடுப்பார்களோ???
http://ocw.mit.edu/courses/mathematics/18-01-single-variable-calculus-fall-2006/video-lectures/
நன்றி.
வாங்க நண்பர் நரேன்,
ReplyDeleteஅடிப்படை சரியாக் புரிந்தால் அனைத்தும் எளிதாகி விடும்.ப்யன்பாட்டீன் அடிப்படையில் அணுகலாம் எனினும் எதிர்காலத்தில் முயற்ச்ப்போம் .இபோது அடிப்படை விடயங்களையே வேறுவிதத்தில் எளிமையாக் புரிய முய்ற்சிக்கிறோம்.
பாருங்கள் பதிவில் கேட்டொம் இரு பரிமாண தளத்திலிரு அடிப்படை அச்சுகளை வைத்து சதுரம் அல்லது செவ்வகம் வரையலாம் என கூறினோம்.இங்கு நான்கு பக்கங்களும் அண்டை பக்கங்கள்க்கு செங்குத்தானவை.ஆனால் தொகைக்கெழுவின் வரையறுப்பின் படி ஒரு ப்க்கம் வளை கோடு இது இருக்க்லாம் ஏன் எனவும் கேடு இருந்தேன் அதன் பதில்
இந்த நுண்கணிதத்தில் மிக சிறிய அளவு dx ,dy, or ds என்பதுதான் மிக முக்கிய விடயம் இது ‘0’ விற்கு அருகில் உள்ள ஆனால் ‘0’ அல்லாத ஒரு positive numbers.
‘ Y’என்பது செவ்வகத்தின் நீளம் dx என்பது அகலம் எனில் பரப்பு y.dx
இது பரப்பின் ஒரு சிறுபகுதி இந்த அனைத்து சிறுப்குதிகளையும் கூட்டுவதுதான் தொகைக்கெழு.
பரப்பு =மிகசிறு செவ்வகங்களின் மொத்த பரப்பு கூட்டல்
A=y1*dx1+y2.dx2…..yn*dxn
வளைகோட்டின் நீளம்[பிதாகரஸ் தேற்றம்] என்பது மிகசிறு நேர்கோடுகளின் நீளத்தின் மொத்த கூட்டல்,
S=ds1+ds2….dsn
Ds^2=dx^2+dy^2
கன அள்வு =மிகசிறிய உருளைகளின் கன அளவின் மொத்த கூட்டல்
Ipi[y1^2.dx1+y2^2.dx2…..yn^2.dxn]
Thank you