Friday, August 24, 2012

தொடர் பின்னக் கூட்டல் அறிவோமா?:Part 1

வணக்கம் நண்பர்களே,

கணிதம் பற்றி பதிவு எழுதி நாளாகி விட்டதால் நமக்கு திடீரெனெ எழுதியே ஆக வேண்டும் என தோன்றியது. சரி எல்லோருக்கும் புரியும் வண்ணம் இருக்க வேண்டும் என தேடல் தொடங்கியது.

நம்க்கு தொடர் கூட்டல் பற்றி தெரியும்.அதாவது தொடர்வரிசை,ஒரு குறிப்பிட்ட தொடர்பில் முன் செல்லும் எண்களின் கூட்டல் பற்றி ஏற்கெனவே ஒரு பதிவில் பார்த்து இருக்கிறோம்.

எ.கா

1+2+3.......

1+2+4+8+16+......

இப்பதிவில் ஒரு தொடர்வரிசை பார்க்கப் போகிறோம் ஆனால் அத்தொடர் பின்னம் சார்ந்து இருக்கும் என்பதும் அது சில சமன்பாடுகளுக்கு தொடர்ந்து விடை அளிக்கும் என்பதுதான் விந்தை!!!!!!

ஒருமுறை கணித மேதை இரமானுஜத்திடம் முனைவர் பி.சி. மஹலனொபிஸ் இந்த சமன் பாட்டுக்கு முழு எண் தீர்வு கண்டுபிடியுங்கள் என்க கேட்க உடனே அவர் இதற்கு ஒரு தொடர் பின்னமே தொடர்ந்து விடைகள் தரும் என கூறினாராம்!

முனைவர் பி.சி. மஹலனொபிஸ் என்பவர் நேரு காலத்தில் இந்தியாவின் ஐந்தாண்டுத் திட்டங்களைத் தீட்டியவர். அவர் இராமானுஜன் கேம்பிரிட்ஜில் வசித்த காலத்தில் அவரும் அங்கு படித்துக் கொண்டிருந்தார். இராமானுஜனுடைய நண்பர்.

இதுதான் அந்த புதிர் x,y க்கு முழு எண்களில் தீர்வு காண வேண்டும்.

$x^2 - 10 y^2 = +1 or -1$

x,y=integers

ஆனால் இராமானுஜன் பிரச்சினையைக் கேட்டவுடனேயே, இதன் விடை ஒரு தொடர் பின்னத்தில் இருக்கிறது என்று கீழ்வரும் தொடர் பின்னத்தை சொன்னார்:

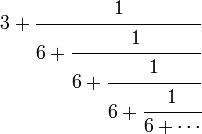
$3 + \cfrac{1}{6+\cfrac{1}{6+\cfrac{1}{6+\cfrac{1}{6+\dotsb}}}}$

இத்தொடர்பின்னத்தின் ஒவ்வொரு ஒருங்கும்(stage) ஒவ்வொரு விடையாகும். முதலாவது ஒருங்கு 3/1. x = 3, y = 1 என்பது முதல் விடை.மஹலனொபிஸின் ஒரே விடைக்கு பதிலாக முடிவுறா எண்ணிக்கையில் தொடர்ந்து பல சரியான விடைகள் கொடுக்கின்றன. ஆக, மேற்படி தொடர்பின்னத்தின் 2வது ஒருங்கு

3 + 1/6 = 19/6.

x =19, y = 6 இரண்டாவது விடை.

$19^2 - 10 * 6^2 = 361 - 360 = 1$

மூன்றாவது ஒருங்கு:

$3 + \cfrac{1}{6+\cfrac{1}{6}}$

இது கொடுக்கும் விடை: x = 117, y = 37[x=numerator,y=denominator]

இதுவும் ஒரு சரியான விடைக‌ள்தான்.

S.No	y	x	X^2-10*y^2	R=x/y	R^2
1	1	3	-1	3	9
2	6	19	1	3.166667	10.02778
3	37	117	-1	3.162162	9.99927
4	228	721	1	3.162281	10.00002
5	1405	4443	-1	3.162278	9.999999
6	8658	27379	1	3.162278	10
7	53353	168717	-1	3.162278	10
8	328776	1039681	1	3.162278	10
9	2026009	6406803	-1	3.162278	10
10	12484830	39480499	1	3.162278	10

இப்போது தொடர்பின்னம்(continued fraction) என்றால் என்ன என்று புரிந்து இருக்கும் என நம்புகிறேன். பின்னத்துக்குள் ,பின்னத்துக்குள்,பின்னத்துக்குள்...பின்னம் என போய்க் கொண்டே இருப்பதுதான் தொடர் பின்னம்.

சரி இது எதுக்கு சகோ விளையாட்டு மாதிரி இருக்கு என்றால் அறிவியலில்(கணிதத்தில்) மூன்று விடயங்களை செய்கிறோம்.

1.அறிந்த விடயம்(known) கொண்டு அறியா விடயம்(unknown) தொடர்புகளில் கணிக்கிறோம்.

2.தொடர்புகளில் உள்ள ஒழுங்குத் தனமை(order) அறிய முயல்கிறோம்.

3.மிகச் சரியாக அறிய முடியாவிட்டால் தோராய(approximation) விடையாவது காண விழைகிறோம்.

இன்னும் கொஞ்சம் விளக்கம் கற்போம்!

Introducing continued fractions

ஒரு இரு படி சமன்பாடு எடுத்துக் கொள்வொம்![Consider the quadratic equation]

$\begin{equation} \htmlimage {} x^2-bx-1=0 \label{A} \end{equation}$

(1)

அதாவது x(x-b)=1

x-b=1/x

[Dividing by 'x' we can rewrite it as]

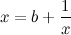$\begin{equation} x=b+\frac1x \end{equation}$

(2)

இபோது சமன்பாடு இரண்டில்'x'கான மதிப்பை அதிலேயே பிரதியிட‌

x=b+1/(b+1/x))

[Now substitute the expression for 'x' given by the right-hand side of this equation for 'x' in the denominator on the right-hand side]:

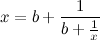$\begin{equation} x=b+\leftb \frac1{b+\frac1x} \rightb \end{equation}$

(3)

ஒரு தொடர்பின்ன சமன்பாடு கிடைக்கும்!!.இது ஒரு முடிவிலி[infinite] தொடர் ஆகும்.ஆனால் இதன் கூடுதல் நிலை மதிப்பு[finite] ஆகலாம்.ஒரு விகிதமுறா [irrational] எண்ணை தொடர்பின்ன முடிவிலி தொடராக எழுத முடியும்!

[We can continue this incestuous procedure indefinitely, to produce a never-ending staircase of fractions that is a type-setter’s nightmare:]

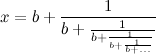$\begin{equation} x=b+\leftb \frac1{b +\frac1{b+\frac1{b+\frac1{b+\ldots }}}} \rightb \label{B} \end{equation}$

(4)

இந்த படிக்கட்டு போன்ற பின்ன அமைப்பு தொடர்பின்னத்தின் எ.கா ஆகும்.

இபோது நாம் எடுத்த முதல் இருஅடி சமன்பாட்டை சூத்திரம் கொண்டு தீர்த்து 'x'ஆக பிரதியிட வேண்டும்.[இதில்தீர்வின் + மதிப்பு மட்டுமே கண்க்கிடப்படுகிறது(ஏன்? எதற்காக? சிந்திக்க மாட்டீர்களா!)]

[This staircase is an example of a continued fraction. If we return to equation 1 then we can simply solve the quadratic equation to find the positive solution for 'x' that is given by the continued fraction expansion of equation 4; it is]

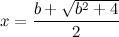$\begin{equation} x=\frac{b+\sqrt {b^2+4}}2 \label{Ba} \end{equation}$

(5)

[Picking ,b=1 we have generated the continued fraction expansion of the golden mean, $\tau$ :]

b=1 எனில் கிடைக்கும் தொடர்பின்னம்!!!

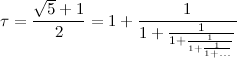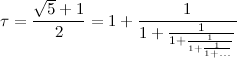! $\begin{equation} \tau =\frac{\sqrt {5}+1}2=1+\frac1{1+\frac1{1+\frac1{1+\frac1{1+\ldots }}}} \label{B1} \end{equation}$ (6)

You can try for b=2,3,4,5,....

சரி இப்போது ஒரு தொடர் பின்னத்தின் மொத்த மதிப்பும் காண முடியும். ஒரு விகிதமுறு(rational),விகித்முறா(irrational) எண்ணை தொடர்பின்னமாகவும் எழுத முடியும்.

10ன் வர்க்க மூலத்தை[square root] தொடர் பின்னமாக எழுதுவோம்!!!

அதற்கான சமன்பாடு இதுதான் எப்படி வந்தது?!!!!!!!!!!!!

x^2-6x-1=0

x=[6+sqrt(36+4)]/2=3+sqrt(10)[புரிந்ததா!!!!! b^2+b=4*10 so b=6]

தொடர் பின்னம் எழுத 'b' மதிப்பு மட்டுமே போதும்.இப்போது தொடர் பின்னப்படி எழுதினால்

sqrt(10)=

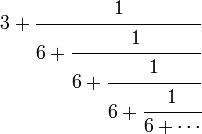
$3 + \cfrac{1}{6+\cfrac{1}{6+\cfrac{1}{6+\cfrac{1}{6+\dotsb}}}}$

[b=6, so b-b/2=3]

ஆமாம் இது இரமானுஜம் சொன்ன விடை ஆயிற்றே!!!!!!!

இதுக்கும் அதுக்கும் என்ன தொடர்பு?????????????

அப்போது ஒவ்வொரு தொடர்பின்னத்துக்கும் இப்படி புதிர் போட முடியுமா?

அந்த முழு எண் புதிரில் இருந்து தொடர்பின்ன விடை எப்படி கொண்டுவருவது?

அல்லது

தொடர் பின்னத்தில் இருந்து முழு எண் புதிர் எப்படி கொண்டு வருவது?

அடுத்த பதிவில் விளக்குவோம்!!!!!!

சந்தேகங்களை வழக்கம் போல் பின்னூட்டம்

நன்றி

(தொடரும்)

http://plus.maths.org/content/chaos-numberland-secret-life-continued-fractions

http://mathworld.wolfram.com/ContinuedFraction.html

Thursday, August 23, 2012

சகோ சுவனப் பிரியன்& கோ விற்கு விளக்கம்: ஆல்கஹால் அற்ற மதுவும் இஸ்லாமில் ஹராமே!!!

[Pictures published by Utusan Malaysia show people to try beer without alcohol]
http://jitlim7.blogspot.com/2011/06/halal-beer-today-whats-tomorrow-halal.html

வணக்கம் நண்பர்களே

இப்பதிவை படிக்கும் இஸ்லாமிய சகோதரர்களுக்கு "அஸ்ஸலாமு அலைக்கும்"சொல்லி நம் பதிவை தொடங்குகிறேன்.

நம் சகோ சுவனப்பிரியன் நமது அன்புக்கும் ,பாசத்துக்கும் உரிய நண்பர் என்பதை அனைவரும் அறிவோம். நாம் மதம் சார்ந்த வரலாறு,வாழ்வியல் ஆகியற்றில் தேடல் சார் ஆய்வு செய்கிறோம், நாம் மதம் சாரா இறை மறுப்பாளர் என்றாலும் நம் கடந்த காலத்தை குறித்த தகவல்கள் தரும் புத்த்கம் என்றவகையில் மத நூல்களை அணுகுகிறோம்.

அதில் உள்ள விடயங்கள் பல இப்போதும் அனைவருக்கும் பொருந்தலாம்,சில பொருந்தாமலும் போகலாம். இஸ்லாம் குறித்த பல பதிவுகள் தமிழ்மணத்தில் வருவதால் அது ஒரு விவாதப் பொருள் ஆவது தவிர்க்க முடியாது.

அந்தவகையில் இஸ்லாம் மது,போதை உண்டாக்கும் பொருள்களை தடை செய்வது நாம் அறிந்த விடயமே!!!.

இஸ்லாமின் ஆரம்ப காலத்தில் மது தடை செய்யப் பட்டது படிப்படியாகவே,எனினும் இறுதியில் போதை உண்டாக்கும் எதுவும் விலக்கப்பட்டதே(ஹாராம் ) என் குரான் அழுத்தம் திருத்தமாக கூறிவிடுகிறது.

முதலில் இறங்கியது

2:219. (நபியே!) மதுபானத்தையும், சூதாட்டத்தையும் பற்றி அவர்கள் உம்மிடம் கேட்கின்றனர்; நீர் கூறும்: “அவ்விரண்டிலும் பெரும் பாவம் இருக்கிறது; மனிதர்களுக்கு (அவற்றில் சில) பலன்களுமுண்டு; ஆனால் அவ்விரண்டிலும் உள்ள பாவம் அவ்விரண்டிலும் உள்ள பலனைவிடப் பெரிது” (நபியே! “தர்மத்திற்காக) எதைச் செலவு செய்ய வேண்டும்” என்று அவர்கள் உம்மிடம் கேட்கின்றனர் “(உங்கள் தேவைக்கு வேண்டியது போக) மீதமானவற்றைச் செலவு செய்யுங்கள்” என்று கூறுவீராக; நீங்கள் சிந்தித்து உணரும் பொருட்டு அல்லாஹ் (தன்) வசனங்களை(யும், அத்தாட்சிகளையும்) இவ்வாறு விவரிக்கின்றான்.

இறுதி கட்டளை(மதுபானம் குறித்த)

5:90. ஈமான் கொண்டோரே! மதுபானமும், சூதாட்டமும், கற்சிலைகளை வழிபடுதலும், அம்புகள் எறிந்து குறி கேட்பதும், ஷைத்தானின் அருவருக்கத்தக்க செயல்களிலுள்ளவையாகும்; ஆகவே நீங்கள் இவற்றைத் தவிர்த்துக் கொள்ளுங்கள் - அதனால் நீங்கள் வெற்றியடைவீர்கள்.

5:91. நிச்சயமாக ஷைத்தான் விரும்புவதெல்லாம், மதுபானத்தைக் கொண்டும், சூதாட்டத்தைக் கொண்டும் உங்களிடையே பகைமையையும், வெறுப்பையும் உண்டு பண்ணி அல்லாஹ்வின் நினைவிலிருந்தும், தொழுகையிலிருந்தும் உங்களைத் தடுத்து விடத்தான்; எனவே, அவற்றை விட்டும் நீங்கள் விலகிக் கொள்ள மாட்டீர்களா?

ஆகவே இப்போது மதுபானம்,சூதாட்டம் இரண்டுமே இஸ்லாமில் ஹராம் என்பதில் ஐயம் வேண்டாம்.

நாம் மதவாதிகளை அதிகம் விமர்சிப்பதே அவர்களின் கருத்து திணிப்பு &இரட்டை வேடமே!!!.

விலக்கப் பட்டது என்றால் மதவாதிகள் செய்யும் முதல் விடயம் அதில் குறுக்கு வழி கண்டுபிடிப்பதே. இஸ்லாமிய மதவாதிகளின் குறுக்கு வழியை அறிய சகோ சுவனப் பிரியனின் பதிவை படிக்க வேண்டுகிறேன்.

அவரின் பதிவின் சாராம்சம்.

http://suvanappiriyan.blogspot.com/2012/08/blog-post_22.html

மதுவில் போதை ஏற்படுத்துவது ஆல்க‌ஹால்,ஆகவே ஆல்கஹால் நீக்கப்பட்ட மதுவைக் குடிக்க்லாம்.

அது எப்படி ஆல்கஹால் இல்லாமல் மதுவரும் என்றால் அழகிய வகையில் விளக்குகிறார் நம் சகோ!!!

’"உடல் வலிக்காக மதுவை குடிக்கிறோம் என்று சொல்பவர்கள் ஆல்கஹால் நீக்கப்பட்ட மதுவை குடிக்கலாமே. அது குடலுக்கு குளிர்ச்சியை தரும். ஆல்கஹால் கலந்த மது குடலை அரிக்க ஆரம்பிக்கும்.

ஹலால் பீர் தயாரிக்கும் நிறுவனங்கள், "இந்த பீரில் 0.01% ஆல்கஹால் இருப்பதாக" விளம்பரம் செய்கின்றது. அதுதான் இஸ்லாமிய மார்க்க அறிஞர்கள் குழு அனுமதிக்கும் ஆல்கஹால் அளவு. இந்த அளவை மீறி ஒரு பானத்தில் ஆல்ஹகால் அதிகமாக கலக்கப்படுமானால் அது போதை ஏற்றக் கூடியதாக மாறி விடுகிறது. இதனை இஸ்லாம் தடை செய்கிறது.”

அது என்ன 0.01% ஆல்கஹால் இருந்தால் ஹராம்(விலக்கப் பட்டது) ஹலால்(அனுமதிக்கப் பட்ட) ஆகி விடும் என்ற கணக்கு?

இதற்கு மத நூல்களில் ஆதாரம் இருக்காது,மார்க்க அறிஞர்களின் விளக்கம் என்பது மதுபானம் என்பது ஏதோஒரு வகையில் சமூகத்தில் தவிர்க்க முடியாதது என்பதை காட்டுவதாகவே எடுக்கலாம்.

நிச்சயமாக இது ஒரு ஏமாற்று வேலையே.

அப்போது இந்த 0.01 வீதம் வரும் வண்ணம் மிக்ஸ்சிங் செய்தால் போதுமான‌து என்ற பொருளும் வருகிறது.ஆகவே மதுபானத் தடை என்பதை மிக்ஸ்சிங் பிரச்சினையாக மாற்றுவதா???

நான் அளவாக சரியா மிக்ஸ்சிங் செய்து குடித்து விட்டு அமைதியாக் தூங்கி விடுவேன் என்பவர்களுக்கும் பொருந்துமா?

காலையில் இருந்து ஏற்கெனவே குடித்த தண்ணீர் அள்வு 90% ஆகவே ஆல்கஹால் இபோது அதிகம் கலக்கலாம் என்னும் பொருளும் கொள்ளலாம்.அப்படி அல்ல என சப்பை கட்டும் சகோதரர்களே. தடை என்றால் முழுதும் தடை அல்லது அது குறித்து விமர்சனம் செய்யாமலாவது இருக்க்லாம்.

இப்படி இரட்டை வேட நகைச்சுவை ஏன்?

சவுதியில் இது அனுமதிக்கப் பட்டுள்ளது என்பதுதானே காரணம்!!!

எனினும் ஒரு முக்கிய இஸ்லாமிய தளம் கூறும் கருத்தினை மட்டும் தமிழாக்கம் செய்து வெளியிடுகிறேன். பிறகு உங்கள் விருப்பம்!!!!!!

http://www.islamawareness.net/Alcohol/non_alcoholic_fatwa.html

Question: Is non-alcoholic beer halal? Can Muslims consume it?

Answer:

In the Name of Allah, Most Gracious, Most Merciful.

All praise and thanks are due to Allah, and peace and blessings be upon His Messenger.

Thanks for your question, and we implore Allah to guide us all to the best way through which we can learn more about what is lawful in order to follow it and what is prohibited in order to refrain from approaching it.

Indeed, Muslims need to understand the process of making so-called non-alcoholic beers or wines. The process to make alcoholic and non-alcoholic beers and wines is the same. Both alcoholic and non-alcoholic beers and wines are haram. Once the beer or the wine is produced, alcohol is extracted from it to make it non-alcoholic. Never is 100 percent of the alcohol removed. The Islamic principle is that if the whole of a thing is haram, the part of it is also haram. By that principle non-alcoholic beers and wines are haram.

Responding to the question, the Islamic Religious Council of Singapore, states the following:

Thank you for your query.

Our position is that non-alcoholic beer is not halal. Our position is based on the premise that

1. It is drunk as an alternative to something which is haram, that is, alcoholic beer.

2. The culture of wine and beer drinking which the drink entails is non-Islamic and, therefore, haram.

Therefore, based on the principle of blocking the doors to transgression in Islamic jurisprudence, non-alcoholic beer is haram.

கேள்வி:ஆல்கஹால் நீக்கப்பட்ட பீர் இஸ்லாமில் அனுமதிக்கப் பட்டதா?

பதில்:அளவற்ற அருளாள‌னும்,எல்லையற்ற இரக்கமுள்ளோனுமாகிய ,ஏக இறைவனின் பெயரால்..

அவனுக்கே எல்லாப் புகழும்,நன்றியும் உரித்தானது!

அமைதியும்,ஆசியும் அவனது தூதர் மீதும் நிலவட்டும்!

உங்களின் கேள்விக்கு ஏக இறைவன் நம்மை மிக சரியாக வழிகாட்டி அதன் மூலம் பின்பற்ற வேண்டியவைகளையும்,விலக்க வேண்டியவைகளையும் அறிய உதவுவானாக!

முஸ்லிம்கள் அறிந்து கொள்ள வேண்டிய விடயம் மதுபானம்( ஆல்கஹால் கொண்ட, நீக்கப்பட்ட) உற்பத்தியில் இரண்டும் ஒரே வகையிலேயே தயாரிக்கப் படுகின்றன.

ஆகவே இரண்டுமே விலக்கப்பட்டது(ஹராம்)

ஆல்கஹாலுடன் உற்பத்தி செய்யப் பட்ட மதுவில் இருந்து ஆல்கஹால் நீக்கப் பட்டு ,ஆல்கஹால் நீகப்பட்ட மது தயாரிக்கப் படுகிறது.

அனைத்து ஆல்கஹாலும் 100% நீக்கப்படும் என்று சொல்ல இயலாது.ஆகவே இஸ்லாமில் ஒரு பொருள் முழுதும் நீக்கப் பட்டது என்றால் ,அதன் சிறிது அளவும் நீக்கப் பட்டதே!!!

இந்த கொள்கையின் அடிப்படையில் ஆல்கஹால் நீக்கப் பட்ட மது ஹராம்!.

சிங்கப்பூர் இஸ்லாமிய கூட்டு அமைப்பின் கருத்தை அறிவோம்

1. ஆல்கஹல் நீக்கப் பட்ட மது ஹராம் ஆன ஆல்கஹால் மதுவிற்கு பதிலாக குடிக்கப்படுகிறது.

2. மதுவகைகள் இஸ்லாமில் தடை செய்யப்பட்டவை.ஆகவே இதுவும் ஹராமே.

http://www.facebook.com/Foodilcious/posts/354875474592044

நாம் சொலவ்து மதவாதிகள் தங்களின் சூழலுக்கு ஏற்ப கருத்து திணிப்பு செய்வதில் மதமும் விதி விலக்கு அல்ல என்பதையே பதிவு செய்கிறோம்.

ஆகவே பிறருக்கு அறிவுரை வழங்குவதை விட தங்களின் இரட்டை வேட போக்கினை கைவிடவே வேண்டுகிறோம்!

மது என்பது பெரும்பாலான் நாட்டு கலாச்சாரங்களில் மிக இயல்பான ஒன்றாகவே கருதப்படுகிறது. முழு மது விலக்கு என்பதும் சாத்தியம் அற்ற ஒன்று என்பதயே இந்த ஆல்கஹால் நீகப்பட்ட மது மீதான விவாதம் காட்டுகிறது.

மது அருந்தாமல் இருப்பது மிக நல்லது. ஆயினும் மது அருந்துபவர்கள் அளவோடு தகுந்த சுகாதார கட்டுப்பாடுகளை கடைப்பிடித்தால் பிரச்சினை இருக்காது.

இதில் ஒரு விடயம் அனைவரும் நன்கு அறியலாம் மதம் சார்ந்த வாழ்வியல் நடைமுறைகள் சூழல் சார்ந்து வித்தியாசப் படும்.

ஆல்கஹால் நீக்கப்பட்ட மது அருந்தலாம் என்பது இஸ்லாமின் படியும் இரு மாறுபட்ட விடைகள் கொண்ட விடயமே!!!!!!!!!!!!

0.01% ஆல்கஹால் கொண்ட மது அருந்தலாம் என்பது நகைப்புக்கு உரிய விடயமே!!!!!!

ஆகவே மது அருந்தாதவர்கள் பிறருக்கு அறிவுரைகள் வாரி வழங்குவதை தவிர்த்து தங்களின் இரட்டை வேடப் போக்கினை பொது தளத்தில் அம்பலப் படுத்த வேண்டாம் எனவே வேண்டுகிறோம்.பொது தளத்தில் விவாதிக்கப் படுவதால் மட்டுமே விமர்சிக்கிறோம். நன்றி

டிஸ்கி
சகோ சுவனனின் கருத்தை ஏற்கும் இறை நம்பிக்கையாளர்களுக்கும் நாம் உதவி செய்யவே விரும்புகிறோம் [நம் கடன் பணி செய்து கிடப்பதே"].

இக்காணொளியில் ஆல்கஹால் நீக்க்கப்பட்ட பீர் வகைகள் பற்றி அழகிய முறையில் விளக்குகின்றார்கள்.அருந்தி மகிழ்க!! Cheers!!!!!!!!!!!!!!!!!!!!1

சமரசம் உலாவும் இடமே!!!!

Friday, August 24, 2012

தொடர் பின்னக் கூட்டல் அறிவோமா?:Part 1

Introducing continued fractions

Thursday, August 23, 2012

சகோ சுவனப் பிரியன்& கோ விற்கு விளக்கம்: ஆல்கஹால் அற்ற மதுவும் இஸ்லாமில் ஹராமே!!!

Non Alcoholic Beer Brands

Earth Clock

visitors