சமரசம் உலாவும் இடமே!!!!: தொடர் பின்னக் கூட்டல் அறிவோமா?:Part 1

Friday, August 24, 2012

தொடர் பின்னக் கூட்டல் அறிவோமா?:Part 1

வணக்கம் நண்பர்களே,

கணிதம் பற்றி பதிவு எழுதி நாளாகி விட்டதால் நமக்கு திடீரெனெ எழுதியே ஆக வேண்டும் என தோன்றியது. சரி எல்லோருக்கும் புரியும் வண்ணம் இருக்க வேண்டும் என தேடல் தொடங்கியது.

நம்க்கு தொடர் கூட்டல் பற்றி தெரியும்.அதாவது தொடர்வரிசை,ஒரு குறிப்பிட்ட தொடர்பில் முன் செல்லும் எண்களின் கூட்டல் பற்றி ஏற்கெனவே ஒரு பதிவில் பார்த்து இருக்கிறோம்.

எ.கா

1+2+3.......

1+2+4+8+16+......

இப்பதிவில் ஒரு தொடர்வரிசை பார்க்கப் போகிறோம் ஆனால் அத்தொடர் பின்னம் சார்ந்து இருக்கும் என்பதும் அது சில சமன்பாடுகளுக்கு தொடர்ந்து விடை அளிக்கும் என்பதுதான் விந்தை!!!!!!

ஒருமுறை கணித மேதை இரமானுஜத்திடம் முனைவர் பி.சி. மஹலனொபிஸ் இந்த சமன் பாட்டுக்கு முழு எண் தீர்வு கண்டுபிடியுங்கள் என்க கேட்க உடனே அவர் இதற்கு ஒரு தொடர் பின்னமே தொடர்ந்து விடைகள் தரும் என கூறினாராம்!

முனைவர் பி.சி. மஹலனொபிஸ் என்பவர் நேரு காலத்தில் இந்தியாவின் ஐந்தாண்டுத் திட்டங்களைத் தீட்டியவர். அவர் இராமானுஜன் கேம்பிரிட்ஜில் வசித்த காலத்தில் அவரும் அங்கு படித்துக் கொண்டிருந்தார். இராமானுஜனுடைய நண்பர்.

இதுதான் அந்த புதிர் x,y க்கு முழு எண்களில் தீர்வு காண வேண்டும்.

$x^2 - 10 y^2 = +1 or -1$

x,y=integers

ஆனால் இராமானுஜன் பிரச்சினையைக் கேட்டவுடனேயே, இதன் விடை ஒரு தொடர் பின்னத்தில் இருக்கிறது என்று கீழ்வரும் தொடர் பின்னத்தை சொன்னார்:

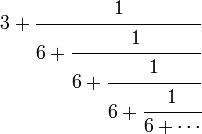
$3 + \cfrac{1}{6+\cfrac{1}{6+\cfrac{1}{6+\cfrac{1}{6+\dotsb}}}}$

இத்தொடர்பின்னத்தின் ஒவ்வொரு ஒருங்கும்(stage) ஒவ்வொரு விடையாகும். முதலாவது ஒருங்கு 3/1. x = 3, y = 1 என்பது முதல் விடை.மஹலனொபிஸின் ஒரே விடைக்கு பதிலாக முடிவுறா எண்ணிக்கையில் தொடர்ந்து பல சரியான விடைகள் கொடுக்கின்றன. ஆக, மேற்படி தொடர்பின்னத்தின் 2வது ஒருங்கு

3 + 1/6 = 19/6.

x =19, y = 6 இரண்டாவது விடை.

$19^2 - 10 * 6^2 = 361 - 360 = 1$

மூன்றாவது ஒருங்கு:

$3 + \cfrac{1}{6+\cfrac{1}{6}}$

இது கொடுக்கும் விடை: x = 117, y = 37[x=numerator,y=denominator]

இதுவும் ஒரு சரியான விடைக‌ள்தான்.

S.No	y	x	X^2-10*y^2	R=x/y	R^2
1	1	3	-1	3	9
2	6	19	1	3.166667	10.02778
3	37	117	-1	3.162162	9.99927
4	228	721	1	3.162281	10.00002
5	1405	4443	-1	3.162278	9.999999
6	8658	27379	1	3.162278	10
7	53353	168717	-1	3.162278	10
8	328776	1039681	1	3.162278	10
9	2026009	6406803	-1	3.162278	10
10	12484830	39480499	1	3.162278	10

இப்போது தொடர்பின்னம்(continued fraction) என்றால் என்ன என்று புரிந்து இருக்கும் என நம்புகிறேன். பின்னத்துக்குள் ,பின்னத்துக்குள்,பின்னத்துக்குள்...பின்னம் என போய்க் கொண்டே இருப்பதுதான் தொடர் பின்னம்.

சரி இது எதுக்கு சகோ விளையாட்டு மாதிரி இருக்கு என்றால் அறிவியலில்(கணிதத்தில்) மூன்று விடயங்களை செய்கிறோம்.

1.அறிந்த விடயம்(known) கொண்டு அறியா விடயம்(unknown) தொடர்புகளில் கணிக்கிறோம்.

2.தொடர்புகளில் உள்ள ஒழுங்குத் தனமை(order) அறிய முயல்கிறோம்.

3.மிகச் சரியாக அறிய முடியாவிட்டால் தோராய(approximation) விடையாவது காண விழைகிறோம்.

இன்னும் கொஞ்சம் விளக்கம் கற்போம்!

Introducing continued fractions

ஒரு இரு படி சமன்பாடு எடுத்துக் கொள்வொம்![Consider the quadratic equation]

$\begin{equation} \htmlimage {} x^2-bx-1=0 \label{A} \end{equation}$

(1)

அதாவது x(x-b)=1

x-b=1/x

[Dividing by 'x' we can rewrite it as]

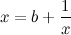$\begin{equation} x=b+\frac1x \end{equation}$

(2)

இபோது சமன்பாடு இரண்டில்'x'கான மதிப்பை அதிலேயே பிரதியிட‌

x=b+1/(b+1/x))

[Now substitute the expression for 'x' given by the right-hand side of this equation for 'x' in the denominator on the right-hand side]:

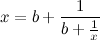$\begin{equation} x=b+\leftb \frac1{b+\frac1x} \rightb \end{equation}$

(3)

ஒரு தொடர்பின்ன சமன்பாடு கிடைக்கும்!!.இது ஒரு முடிவிலி[infinite] தொடர் ஆகும்.ஆனால் இதன் கூடுதல் நிலை மதிப்பு[finite] ஆகலாம்.ஒரு விகிதமுறா [irrational] எண்ணை தொடர்பின்ன முடிவிலி தொடராக எழுத முடியும்!

[We can continue this incestuous procedure indefinitely, to produce a never-ending staircase of fractions that is a type-setter’s nightmare:]

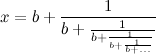$\begin{equation} x=b+\leftb \frac1{b +\frac1{b+\frac1{b+\frac1{b+\ldots }}}} \rightb \label{B} \end{equation}$

(4)

இந்த படிக்கட்டு போன்ற பின்ன அமைப்பு தொடர்பின்னத்தின் எ.கா ஆகும்.

இபோது நாம் எடுத்த முதல் இருஅடி சமன்பாட்டை சூத்திரம் கொண்டு தீர்த்து 'x'ஆக பிரதியிட வேண்டும்.[இதில்தீர்வின் + மதிப்பு மட்டுமே கண்க்கிடப்படுகிறது(ஏன்? எதற்காக? சிந்திக்க மாட்டீர்களா!)]

[This staircase is an example of a continued fraction. If we return to equation 1 then we can simply solve the quadratic equation to find the positive solution for 'x' that is given by the continued fraction expansion of equation 4; it is]

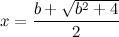$\begin{equation} x=\frac{b+\sqrt {b^2+4}}2 \label{Ba} \end{equation}$

(5)

[Picking ,b=1 we have generated the continued fraction expansion of the golden mean, $\tau$ :]

b=1 எனில் கிடைக்கும் தொடர்பின்னம்!!!

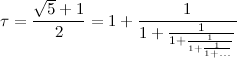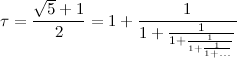! $\begin{equation} \tau =\frac{\sqrt {5}+1}2=1+\frac1{1+\frac1{1+\frac1{1+\frac1{1+\ldots }}}} \label{B1} \end{equation}$ (6)

You can try for b=2,3,4,5,....

சரி இப்போது ஒரு தொடர் பின்னத்தின் மொத்த மதிப்பும் காண முடியும். ஒரு விகிதமுறு(rational),விகித்முறா(irrational) எண்ணை தொடர்பின்னமாகவும் எழுத முடியும்.

10ன் வர்க்க மூலத்தை[square root] தொடர் பின்னமாக எழுதுவோம்!!!

அதற்கான சமன்பாடு இதுதான் எப்படி வந்தது?!!!!!!!!!!!!

x^2-6x-1=0

x=[6+sqrt(36+4)]/2=3+sqrt(10)[புரிந்ததா!!!!! b^2+b=4*10 so b=6]

தொடர் பின்னம் எழுத 'b' மதிப்பு மட்டுமே போதும்.இப்போது தொடர் பின்னப்படி எழுதினால்

sqrt(10)=

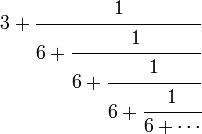
$3 + \cfrac{1}{6+\cfrac{1}{6+\cfrac{1}{6+\cfrac{1}{6+\dotsb}}}}$

[b=6, so b-b/2=3]

ஆமாம் இது இரமானுஜம் சொன்ன விடை ஆயிற்றே!!!!!!!

இதுக்கும் அதுக்கும் என்ன தொடர்பு?????????????

அப்போது ஒவ்வொரு தொடர்பின்னத்துக்கும் இப்படி புதிர் போட முடியுமா?

அந்த முழு எண் புதிரில் இருந்து தொடர்பின்ன விடை எப்படி கொண்டுவருவது?

அல்லது

தொடர் பின்னத்தில் இருந்து முழு எண் புதிர் எப்படி கொண்டு வருவது?

அடுத்த பதிவில் விளக்குவோம்!!!!!!

சந்தேகங்களை வழக்கம் போல் பின்னூட்டம்

நன்றி

(தொடரும்)

http://plus.maths.org/content/chaos-numberland-secret-life-continued-fractions

http://mathworld.wolfram.com/ContinuedFraction.html

18 comments:

வானம்August 24, 2012 at 12:40 PM
சின்ன சந்தேகம் கூட இல்லை. ஏனென்றால் எனக்கு எதுவுமே புரியவில்லை. திரும்பத்திரும்ப படித்து புரிந்துகொள்ள முயற்சிக்கிறேன்.
ReplyDelete
Replies
சார்வாகன்August 24, 2012 at 2:55 PM
ஹா ஹா ஹா
வாங்க சகோ வானம்!
அருமை சகோ .உண்மை பேசுவதற்கு பாராட்டுக்கள்.

ஒரு பின்னம் அதுக்கு கிழே அதே பின்னம் அதுக்கு கிழே அதே பின்னம்....அப்படியே போகுது .இந்த மாதிரி விளையாட்டா எழுதுவதிலும் ஒரு ஒழுங்கு இருக்கிறது.

அவ்வள்வுதான் !

முடிவிலி பின்ன தொடருக்கு நிலை எண் மதிப்பு காண முடியும்.

அல்லது

ஒரு நிலை எண்ணுக்கு முடிவிலி தொடர் பின்னம் எழுத முடியும்!

என்ன செய்கிறோம் என்பது அறிந்தால் எப்படி செய்வது என்பது தானாக வந்துவிடும்!!

மீண்டும் பாராட்டுகிறேன்!

நன்றி
ReplyDelete
Replies
AnonymousAugust 25, 2012 at 9:19 AM
கணிதமா ? எனக்கு கொஞ்சம் வேப்பங்காய் தான். ஆனால் என்னவோ பன்னிராண்டாம் வகுப்பில் 88 % வந்துடுச்சு !!! ஆனால் அதுக்கப்புறம் சயின்ஸுக்கு தாவிட்டேன் !!!

ஜெமா ரெண்டு மூணு தடவைப் படித்த பின் தான் விளங்கி கொண்டேன்.. கணிதம் நமக்குக் கொஞ்சம் கடிக்கும் அதனால் தான் ..
ReplyDelete
Replies
UnknownAugust 25, 2012 at 10:45 AM
வணக்கம் சகோ,

ஸ்ஸ்ஸ்ஸப்ப்பா.....முடியல கணக்குப் பரீட்சையில் நான் ரொம்ப கணக்குப் பார்த்துதான் எழுதுவேன். இருப்பினும் வாழ்த்துக்கள்.

இனியவன்...
ReplyDelete
Replies
சார்வாகன்August 25, 2012 at 6:17 PM
வாங்க சகோ இனியவ‌ன்,

இது ஒன்றும் பெரிய விடயம் அல்ல. நமக்கு கல்வி மனபாடம் செய்து மதிப்பெண் வாங்கும் உத்தியாக சொல்லிக் கொடுக்கப் பட்டதே காரணம்.

இது ஒரு இருபடி சமன்பாடு( 10 ஆம் வகுப்பு கணிதம்) சார்ந்த கணிதம் அவ்வளவுதான்!.நாம் அறிந்த விடயங்களிலேயே பல் நூக்கமான விடயங்கள் உண்டு!!!

தமிழ் பதிவர் மாநாட்டு டிவிட்ட‌ரில் சந்திப்போம். உரையாடுவோம்!

நன்றி
ReplyDelete
Replies
?August 25, 2012 at 7:28 PM
கேள்விகள் கேனத்தனமாக இருப்பின் மன்னிக்கவவும்.யாம் முன்றாம் கிளாஸ் பெயில், ஆஃப்டர் மூணு அட்டம்ட் என்பதை நினைவில் கொள்ளவும்.

1. இருபடி சமன்பாடுகளைவிட தொடர் பின்னம் மிகவும் கடினமாக இருக்கிறது. பிறகு எதற்காக அதை தீர்க்க தொ.பி த்தை உபயோகப்படுத்த வேண்டும்?

2. சமன்பாடு 4 லிருந்து ஸ்கொயர் ரூட்டுடனான சமன்பாடு 5 எப்படி வந்தது என சுருக்கமாக விளக்க இயலுமா?. இணையதளத்திலும் இப்படி ஜம்ப் பண்ணிவிட்டார்கள்.

நன்றி
ReplyDelete
Replies
சார்வாகன்August 25, 2012 at 7:44 PM
வாங்க சகோ நந்தவந்த்தான்
கணிணி முன்னல் உட்கார்ந்து சிந்தித்தால் இப்படித்தான் சிந்திப்போம்.
//1. இருபடி சமன்பாடுகளைவிட தொடர் பின்னம் மிகவும் கடினமாக இருக்கிறது. பிறகு எதற்காக அதை தீர்க்க தொ.பி த்தை உபயோகப்படுத்த வேண்டும்?/

அப்போது 6ஆம் நூற்றாண்டு ஆர்யபட்டா நிலையை யோசியுங்கள்.

அப்போது சமன்பாடுகளை தீர்ப்பது மிக கடினம் என்பதால், இந்த முறை அதிக முயற்சி தேவப்பட்டாலும் ஏற்கப் பட்டது.
//2. சமன்பாடு 4 லிருந்து ஸ்கொயர் ரூட்டுடனான சமன்பாடு 5 எப்படி வந்தது என சுருக்கமாக விளக்க இயலுமா?. இணையதளத்திலும் இப்படி ஜம்ப் பண்ணிவிட்டார்கள்.//

(5) ஆம் சமன்பாடு ஒரு quadratic eauations ஐ தீர்க்க உதவும் சூத்திரம்,
http://en.wikipedia.org/wiki/Quadratic_equation
இது வேறு.இதனை (4)அதனோடு சமப்படுத்துகிறார்கள்!!!!
ReplyDelete
Replies
சார்வாகன்August 25, 2012 at 8:12 PM
http://www-history.mcs.st-and.ac.uk/Biographies/Aryabhata_I.html

Next we look briefly at some algebra contained in the Aryabhatiya. This work is the first we are aware of which examines integer solutions to equations of the form by = ax + c and by = ax - c, where a, b, c are integers. The problem arose from studying the problem in astronomy of determining the periods of the planets. Aryabhata uses the kuttaka method to solve problems of this type. The word kuttaka means "to pulverise" and the method consisted of breaking the problem down into new problems where the coefficients became smaller and smaller with each step. The method here is essentially the use of the Euclidean algorithm to find the highest common factor of a and b but is also related to continued fractions.

Aryabhata gave an accurate approximation for π. He wrote in the Aryabhatiya the following:-

Add four to one hundred, multiply by eight and then add sixty-two thousand. the result is approximately the circumference of a circle of diameter twenty thousand. By this rule the relation of the circumference to diameter is given.

This gives π = 62832/20000 = 3.1416 which is a surprisingly accurate value. In fact π = 3.14159265 correct to 8 places.
_____
We now look at the trigonometry contained in Aryabhata's treatise. He gave a table of sines calculating the approximate values at intervals of 90°/24 = 3° 45'. In order to do this he used a formula for sin(n+1)x - sin nx in terms of sin nx and sin (n-1)x. He also introduced the versine (versin = 1 - cosine) into trigonometry.

Other rules given by Aryabhata include that for summing the first n integers, the squares of these integers and also their cubes. Aryabhata gives formulae for the areas of a triangle and of a circle which are correct, but the formulae for the volumes of a sphere and of a pyramid are claimed to be wrong by most historians. For example Ganitanand in [15] describes as "mathematical lapses" the fact that Aryabhata gives the incorrect formula V = Ah/2 for the volume of a pyramid with height h and triangular base of area A. He also appears to give an incorrect expression for the volume of a sphere. However, as is often the case, nothing is as straightforward as it appears and Elfering (see for example [13]) argues that this is not an error but rather the result of an incorrect translation.
________
The Aryabhatiya of Aryabhata
An Ancient Indian Work on Mathematics and Astronomy (Large Print Edition) (Hardcover)
*********
பாருருங்கள் 500 களில் நம் முன்னோரின் அறிவு திறம்!!!.

இவர் கண்டு பிடித்த விடயங்களை பிறரும் சாராமல் கண்டுபிடித்த‌தும் அறியலாம்.

அது என்னமோ சமஸ்கிருதத்தில் இருந்தால் நம் அரைகுறைப் பகுத்தறிவுகள்க்கு அறிவியல்,நாத்திகம் கூட தெரிய மாட்டென் என்கிறது!!

ஆர்யபட்ட என்னும் ஆரிய இனவாதி என்று சொன்னாலும் சொல்வார்கள்.

அக்கால்த்தில் சமஸ்கிருதம்(வடமொழி) ,தமிழ் கருத்து பரிமாற்றம் மிக எளிதாக் இயல்பாக இருந்ததால் இதே போன்ற கணிதம் கொண்ட தமிழ் நூல்களும் நிச்சயம் இருக்கும் என்பது என் நம்பிக்கை.

அல்லது ஆர்யப்ட்ட கூட தமிழில் ஏதேனும் எழுதி இருக்க்லாம்!

எவராவது தமிழாக்கம் செய்து இருப்பார்கள்!!

பழமை எதையும் அறிய மாட்டோம்,பாதுகாக்க மாட்டோம்,தமிழ் தமிழ் என வெற்றுக் கூச்சல் மட்டும் போடுவோம்!

நன்றி!!!!!

http://www.betterworldbooks.com/the-aryabhatiya-of-aryabhata-id-1169887783.aspx
ReplyDelete
Replies
சார்வாகன்August 25, 2012 at 8:17 PM
You can download Aryabhatta book here
http://archive.org/details/TheAryabhatiyaOfAryabhata
ReplyDelete
Replies
?August 25, 2012 at 9:24 PM
விளங்கங்களுக்கு நன்றி. சின்ன விசயங்கள்தான் விடையாக இருக்கும் என ஊகித்துதான் பின்னூட்டத்தின் முதல் வரியை எழுதியிருந்தேன்.

ஆரியபட்டா உண்மையிலேயே இந்தியர்களை பெருமை கொள்ள வைக்கும் ஒரு கணிதவியலர். ஆனால் வெள்ளையர்கள் தாங்கள் மட்டும்தான் பெரிய புடுங்கிகள் எனும் எண்ணமுடையவர்கள் ஆதலால் கிரேக்கர்களுக்கு கொடுத்த மரியாதையை இந்திய அரேபிய கணிதவியல் அறிஞர்களுக்கு தர தவறிவிட்டார்கள்.

//அது என்னமோ சமஸ்கிருதத்தில் இருந்தால் நம் அரைகுறைப் பகுத்தறிவுகள்க்கு அறிவியல்,நாத்திகம் கூட தெரிய மாட்டென் என்கிறது!!//

நன்றாக சொன்னீர்கள். பெரியாரின் மீது நான் வைக்கும் விமர்சனம் இதுதான். அவர் பார்பனர்களின் இனவெறிக்கு பதிலாக இனவெறியையே முன்னிறுத்தினார். இனவெறியை எந்த ரூபத்திலும் எதிர்க்க வேண்டும். பார்பனர்களை ஒழிக்க இந்திய பாரம்பரியத்தை, அறிவு பொக்கிசங்களை அழிக்க நினைத்தார். மேலும் ஆத்திக முட்டாள்களுக்கு போட்டியாக நாத்திக முட்டாள் கும்பலை வளர்த்துவிட்டார்.

ஏதோ உங்களைப் போன்ற சிலர் தமிழுக்கு அறிவியல் கணிதம் இவற்றே கொணர நினைக்கிறீர்கள். ஆனால், முன்பு சம்ஸ்கிருதம் இப்போது ஆங்கிலம் இவைதான் இந்தியாவில் அறிஞர் மொழியாக உள்ளது.தமிழுக்கு பரிதாபமான நிலைதான். இவர்களுக்கு உண்மையில் தமிழ் பற்று இருப்பின் பிற மொழி எதிர்ப்பினை விட்டுவிட்டு தமிழுக்கு அறிவியலை கொணரட்டும், ஆனால் அந்த அளவுக்கு அறிவு இல்லாததால்தான் இந்த வெற்றுக்கூச்சல்!
ReplyDelete
Replies
சார்வாகன்August 25, 2012 at 9:36 PM
//தமிழ் பற்று இருப்பின் பிற மொழி எதிர்ப்பினை விட்டுவிட்டு தமிழுக்கு அறிவியலை கொணரட்டும்//
சகோ நந்தவனத்தான்,
நம் நோக்கம் இதுதான்.உங்கள் போன்ற ஆர்வம் உள்ளோரின் ஊக்கத்தால் இன்னும் தமிழுக்கு பிற நாட்டு நல்லறிஞர் சாத்திரம் அளிப்போம்!

இன்னும் பலர் அறிவியல் சார் தமிழ் பதிவுகள் எழுத வேண்டும்!.

மதவதிகளின் போலி அறிவியல் பிரச்சாரங்கள் முறியடிக்கப் பட வேண்டும்!
********
நாம் சொல்வது பெரியார் வாழ்ந்த சூழல்,காலத்தை பிரதிபலித்தார்.அவ்வள்வுதான்!அவரின் சிந்தனை செயல்களில் பல இபோதும் ஏற்புடையன்.சூழல் சார்ந்து சில இப்போது பொருந்தாதவை!

ஆனால் அவர் வழி வந்தவர்களின் நடவ்டிக்கைகள் எந்த விதத்திலும்,தமிழுக்கோ,நாத்திகத்திற்கோ வலு சேர்க்கவில்லை என உறுதியாக கூறுகிறோம்!

அவர்களின் நாத்திகம் சிறுபான்மை மதவாதிகளால் நன்கு பயன்படுத்திக் கொள்ளப் பட்டது என்பதுதான் உண்மை!.

நாம் நம்மால் இயன்ற வரை ஹி ஹி!!!!!!!!!!11
ReplyDelete
Replies
UnknownAugust 26, 2012 at 8:18 AM
சகோ.சார்வாகன்,
//அவர்களின் நாத்திகம் சிறுபான்மை மதவாதிகளால் நன்கு பயன்படுத்திக் கொள்ளப் பட்டது என்பதுதான் உண்மை!.//

100%உண்மைதான் அத‌னால்தான் நாத்திக‌ விவாத‌த்தில் கூட‌ அவ‌ர்க‌ளால் ச‌ரிவ‌ர‌ விவாதிக்க‌ முடிய‌வில்லை. ச‌ரியான‌ புரிந்துண‌ர்வின்றி எதிர்கொண்டு நாத்திக‌த்தையே கேள்விக்குறியாக்கிவிட்ட‌ன‌ர் என்ப‌தே என் க‌ருத்து.

இனிய‌வ‌ன்...
ReplyDelete
Replies
UnknownAugust 26, 2012 at 8:25 AM
சகோ.சார்வாகன்,
//அவர்களின் நாத்திகம் சிறுபான்மை மதவாதிகளால் நன்கு பயன்படுத்திக் கொள்ளப் பட்டது என்பதுதான் உண்மை!.//

100%உண்மைதான் அத‌னால்தான் நாத்திக‌ விவாத‌த்தில் கூட‌ அவ‌ர்க‌ளால் ச‌ரிவ‌ர‌ விவாதிக்க‌ முடிய‌வில்லை. ச‌ரியான‌ புரிந்துண‌ர்வின்றி எதிர்கொண்டு நாத்திக‌த்தையே கேள்விக்குறியாக்கிவிட்ட‌ன‌ர் என்ப‌தே என் க‌ருத்து.

இனிய‌வ‌ன்...
ReplyDelete
Replies
ராஜ நடராஜன்August 26, 2012 at 5:06 PM
கணக்கா!நல்லவேளை நான் வவ்வாலின் தொடர் பின்னூட்டத்திலிருந்து முந்தைய பதிவுக்கு மறுபடியும் பின்னூட்டம் போட்டுட்டு எஸ்கேப்.

அப்படியும் வரலாற்றை மறக்க முடியுமா?ராமனுஜத்திற்கும்,தபால் தலைக்கும் வந்தனம் செய்வோம்.
ReplyDelete
Replies
ராஜ நடராஜன்August 26, 2012 at 5:21 PM
திரும்ப போகலாம்ன்னு பார்த்தால் பெரியார் வேற கண்ணில் பட்டுட்டாரே!விட்டுட்டுப் போக மனமில்லை.

பெரியார் வாழ்ந்த காலகட்டத்துடன் ஒப்பிட்டுப் பார்க்கும் போது திராவிட கழகமும்,தி.மு.கவின் ஆட்சி பீட துவக்க காலம் வரையிலான சமூக கருத்துக்கள் தமிழகத்தின் சமூக மாற்ற காலம் என்பதில் ஐயமில்லை.பெரியாரின் மறைவுக்குப் பிறகு வீரமணி திராவிட கழகத்தை ஹைஜாக் செய்ததும்,சமூக போராட்டங்களை திராவிட கழகத்தினர் முன்னெடுத்த போதும் கூட திராவிட கழகம் பிரிந்து நின்று செயல்பட்டதில் தன் வலுவை இழந்து விட்டது.போதாக் குறைக்கு இலங்கையில் சகோதர யுத்தம் பற்றி பேசும் கலைஞரின் ஆட்சி முறையில் தி.மு.கவும் சகோதர யுத்தத்தால் பிளவு ப்ட்டு....மிச்ச சோகக் கதைகள்தான் ஊரறிந்த விசயமாச்சே.

ஏதோ பழைய காலத்து கட்டிடம்ங்கிற மாதிரி இன்னும் கொஞ்சம் தாங்கிப்பிடிச்சுகிட்டு ஓடுகிற மாதிரி தெரியுது."இரண்டு" ஆணிவேரும் கழண்ட பின்னர் தமிழகம் எப்படி பயணம் செய்யும் என்பதை யாராவது நோஸ்டர்டாமஸ் செய்தால் நல்லது.
ReplyDelete
Replies
சார்வாகன்August 27, 2012 at 4:02 AM
வாங்க சகோ இராஜ நட,

நமக்கு பல பரிமாணம் உண்டு.பெரியாரும் பல பரிமாணம் உடையவர். நாம் கணிதம் எழுதினாலும் அதில் ஏதேனும் நாத்திக உள்குத்து இருக்கிறதோ என்றே ஆத்திக சகோக்கள் அஞ்சி ஒதுங்கிறார்.

நாம் பெரியாரிடம் இருந்து கற்ற விடயம் பல உண்டு.பெரியாரில் நம்க்கு பிடித்த பரிமாண‌த்தை எடுப்பதும்,அவரை வைத்து அரசியல் வியாபாரம் செய்யும் போலி நாத்திகவாதிகளிடம் இருந்து அவரையும்,நாத்திகத்தையும் விடுவிப்பதே நம் பணி!!!

பெரியார் அரசியலுக்கு வர விரும்பவில்லை என்பதே அவரின் உயர் குணத்தை காட்டி விடுகிறது. தி.மு.க வை விட காமராசர் தலைமையில் இருந்த‌ காங்கிரசையே அவர் ஆதரித்தார் என்பதும் வரலாறு.

//ஏதோ பழைய காலத்து கட்டிடம்ங்கிற மாதிரி இன்னும் கொஞ்சம் தாங்கிப்பிடிச்சுகிட்டு ஓடுகிற மாதிரி தெரியுது."இரண்டு" ஆணிவேரும் கழண்ட பின்னர் தமிழகம் எப்படி பயணம் செய்யும் என்பதை யாராவது நோஸ்டர்டாமஸ் செய்தால் நல்லது.//

"மாற்றம் ஒன்றே மாற்றமில்லாதது"

நன்றி!!!!!!!!!
ReplyDelete
Replies
டி.என்.முரளிதரன் -மூங்கில் காற்று September 1, 2012 at 6:37 AM
நன்பரே!தொடர் பின்னத்தை நன்கு விளக்கி இறுக்கி இருக்கிறீர்கள். அடுத்த பதிவில் சில ஐயங்கள் இருந்ததால் இந்தப் பதிவுக்கு வந்து தெரிந்து கொண்டேன். உங்கள் பணி பாராட்டுதற்குரியது. நீங்கள் கணிதல் பற்றி எழுதுவதை புரிந்தாலும் புரியாவிட்டாலும் படித்து வருகிறேன். தொடர்க.
ReplyDelete
Replies