சமரசம் உலாவும் இடமே!!!!: பூமிப் பந்து: பெரிய வட்டம்: குறுக்குப் பாதை!!!

Saturday, February 16, 2013

பூமிப் பந்து: பெரிய வட்டம்: குறுக்குப் பாதை!!!

வணக்கம் நண்பர்களே,

இப்பதிவில் பூமியின் இரு இடங்களுக்கு இடையே உள்ள தூரம் அறியும் முறை கற்போம்.

இது எதற்கு என்றால் சார்பியலை கணிதம் மூலம் கற்றல் செய்கிறோம் அல்லவா, அதில் ஒரு அடிப்படை என வையுங்கள். மெதுவாக சென்று அனைத்தையும் இணைப்போம்!!

ஒரு வரைபடத் தாள் இரு பரிமாணம் உள்ளது அதில் இரு புள்ளிகள் இடையே உள்ள குறைந்த பட்ச தூரம் என்ன என்றால் அனைவருக்கும் சூத்திரம் தெரியும்!!

முதல் புள்ளி=[x1,y1]

இரண்டாம் புள்ளி=[x2,y2]

தூரம்=

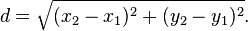$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}.$ [Two dimension]

$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2+ (z_2-z_1)^2}$ [Three Dimension]

Proof for two dimension

சரி இதுதான் தெரியுமே என்கிறீர்களா!!

இப்போது நம் பூமிப் பந்தில் ஒரு இடத்தை இரு ஆயத்தொலைகளான அட்சக் கோடு[latitude] , தீர்க்க கோடு [Longitude] மூலம் குறிக்கிறோம்.

இப்போது பூமிப் பந்தில் இரு புள்ளிகளுக்கு இடையே உள்ள குறைந்த பட்ச தூரம் அறிவது எப்படி?

இரு பரிமாண சமதளத்தில் இரு புள்ளிகளுக்கு இடையே உள்ள குறைந்த பட்ச தூரம் நேர் கோடு எனில், முப்பரிமாண கோளத்தில் குறைந்த பட்ச தூரம் என்பது பெரிய வட்ட வில்[Great circle arc] ஆகும்.

பெரிய வட்டம் எனறால் இந்த இருபுள்ளிகளையும் இணைக்கும் வண்ணம் கோள[பூமி] மைய‌த்தில் இருந்து வரையப்படும் வட்டம் ஆகும்.[எப்பூடீ சகோ என்றால் சிந்திக்க மாட்டீர்களா??!!]

இது கோளத்தை(பூமியை) இரண்டாக பிரிக்கும்.

http://en.wikipedia.org/wiki/Great_circle

இதில் அட்சக் கோடு(latitude) என்பது பூமியின் மீது கிடைமட்டமாக கிழக்கில் இருந்து மேற்கு செல்லும் கற்பனைக் கோடுகள் ஆகும்.நிலநடுக்கோடு என்பது 0 டிகிரி, வடதுருவம் 90 டிகிரி ,தென் துருவம் ‍டிகிரி ஆகும்.

இது φ என்னும் குறியீட்டால் அறியப் படுகிறது . -90=<φ=<90 degrees.

இதில் தீர்க்க கோடு [Longitude] என்பது பூமியின் மீது மேல் கீழாக‌ வட துருவத்தில் இருந்து தென் துருவம் செல்லும் கற்பனைக் கோடுகள் ஆகும்.

இது λ என்னும் குறியீட்டால் அறியப்படுகிறது . -180=<λ=<180 degrees.

லண்டன் ராயல் ஆய்வகம் வழி செல்லும் கிரீன்விச் தீர்க்க கோடு 0 டிகிரி ஆகும்.நேரமும் இதன் அடிப்படையில் கண்க்கிடப் படுகிறது. கிழக்கு, வடக்கு நேர் எண் மதிப்பும்[positive], மேற்கு, தெற்கு எதிர் எண் [negative]மதிப்பும் கொடுக்கிறோம்.

இப்போது பூமியின் இரு இடங்களின் அட்ச ,தீர்க்க கோடு மதிப்பு அறிந்தால் அவைகளுக்கு இடையே உள்ள தூரம் காணும் சூத்திரம் அறிவோம்.

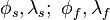$\phi_s,\lambda_s;\ \phi_f,\lambda_f\;\!$ என்பவை தொடங்கும்(Starting), சேரும்(Final) இடங்களின் அட்ச,தீர்க்க கோடுகள் ஆகட்டும்.

;இடைப் பட்ட கோண அளவு $\Delta\widehat{\sigma}\;\!$ , காணும் சூத்திரம்

${\color{white}\Big|}\Delta\widehat{\sigma}=\arccos\big(\sin\phi_s\sin\phi_f+\cos\phi_s\cos\phi_f\cos\Delta\lambda\big).\;\!$

$\Delta\widehat{\sigma}\;\!$ unit is Radian[ PI Radians=180 degrees]

Δλ=λ_s- λ_f

கோண அளவு ரேடியன்களின் உள்ள போது ஆரத்தை பெருக்கினால் தூரம் கிட்டும்.

$d = r \, \Delta\widehat{\sigma}.\,\!$

r = 6,371,009 metres

Worked example

For an example of the formula in practice, take the latitude and longitude of two airports:

Nashville International Airport (BNA) in Nashville, TN, USA: N 36°7.2', W 86°40.2'
Los Angeles International Airport (LAX) in Los Angeles, CA, USA: N 33°56.4', W 118°24.0'

First convert the co-ordinates to decimal degrees

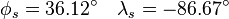
BNA: $\;\phi_s=36.12^\circ \quad\lambda_s=-86.67^\circ\;\!$
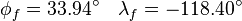
LAX: $\;\phi_f=33.94^\circ \quad\lambda_f=-118.40^\circ\;\!$

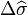Plug these values into the spherical law of cosines: $\cos\Delta\widehat{\sigma}=\sin\phi_s\sin\phi_f+\cos\phi_s\cos\phi_f\cos\Delta\lambda\,\!$

$\Delta\widehat{\sigma}$ comes out to be 25.958 degrees, or 0.45306 radians, and the great-circle distance is the assumed radius times that angle: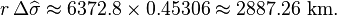

$r\,\Delta\widehat{\sigma}\approx 6372.8 \times 0.45306 \approx 2887.26\mbox{ km}.\;\!$

இப்பதிவில் சொல்லியது மிகவும் எளிதான தோராய[approximate] கணக்கீட்டுமுறை. பூமியை ஒரு கோளமாக[Sphere] அனுமானித்தே இந்த சூத்திரம் வடிவமைக்கப் பட்டது.

இந்த சூத்திரம் எப்படி வந்தது என ஒருவராவது விரும்பினால் அடுத்த பதிவில் எழுதுகிறேன்!!

நன்றி!!!

http://en.wikipedia.org/wiki/Great-circle_distance

11 comments:

ப.கந்தசாமிFebruary 16, 2013 at 5:21 AM
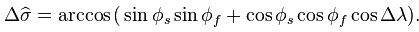
என்க்கு மிகவும் பிடித்த, தெரிந்து கொள்ள விரும்பிய, கணித விளக்கம். ஆனா மேலோட்டமாப் பாத்ததுக்கே தலை சுத்துதே, நான் எப்ப ஆழமாப் படிச்சுப் புரிஞ்சுக்கிறது? அடுத்த ஜன்மத்தில் முயற்சிக்கிறேன்.
ReplyDelete
Replies
டி.என்.முரளிதரன் -மூங்கில் காற்று February 16, 2013 at 8:23 AM
S=r x angle in radians என்று படித்திருக்கிறேன்.
நிருபணத்தை நிச்சயம் சொல்லுங்கள் ஆற்றலரசு. தெரிந்து கொள்ள ஆவலாக இருக்கிறேன்.உங்கள் பரிணாமப் பதிவுகளைவிட இது போன்ற பதிவுகளையே விரும்பிப் படிக்கிறேன்.உங்கள் நுண்ணறிவு பிரமிக்க வைக்கிறது.
ReplyDelete
Replies
நம்பள்கிFebruary 16, 2013 at 9:04 AM
இந்த தலைப்பு, "பந்து: பெரிய வட்டம்: குறுக்குப் பாதை" பார்த்து நம்ம விஷயம் என்று வந்தால்...

அய்யா அப்பீட்! கொல்லன் பட்டரையிலே ஈக்கு என்ன வேலை?

சாமி! படிக்கும் படியா எதாவது பதிவு போடுங்க!
ReplyDelete
Replies
Jayadev DasFebruary 16, 2013 at 10:19 AM
\\உங்கள் நுண்ணறிவு பிரமிக்க வைக்கிறது.\\ இப்படி உசுப்பேத்தி உசுப்பேத்தியே ரணகளமாக்கிட்டாங்கலேடா................ [ முரளீதரன் Sorry Brother, வாய வச்சுகிட்டு சும்மா இருக்க முடியலே!! ]
ReplyDelete
Replies
GanesanFebruary 16, 2013 at 1:46 PM
நல்ல பதிவு சார்வாகன். புரியும் படி அருமையாய் இருந்தது. நன்றி.

அதுவும் அந்த பூமி பந்தில் ஒரு பகுதியை, ஒரு ஆப்பிளை எப்படி வேட்டுவோமோ அப்படி வெட்டி, காட்டிய படம் இந்த " -90=<φ=<90 degree, -180=<λ=<180 degrees" விஷயங்களை அழகாய் விளக்கிவிட்டது. இல்லாவிடில் எனக்கு சற்று கஷ்டமாக தான் இருந்திருக்கும். சும்மாவா சொல்கிறார்கள் ஒரு படம் ஆயிரம் வார்த்தைக்கு சமானம் என்று.

சூத்திரம் எப்படி வந்தது என்ற பதிவையும் எப்போது முடியுமோ அப்போது இடுங்கள். முடிந்தால் படங்களோடு ;)
ReplyDelete
Replies