அறிவார்ந்த வடிவமைப்பு அறிவோம்: பகுதி 9:பரிணாம செயலாக்க கணிதம் .

வணக்கம் நண்பர்களே,

இதுவரை அ.வ் கொள்கையாக்கத்தின் எ.சி.வ[எளிமைப் படுத்த முடியாத சிக்க்லான வடிவமைப்பு] பற்றி கற்று வந்தோம்.அதன் பிதாமகன் மிக்கேல் பெஹே அவருடைய எடுத்துக் காட்டுகள் மற்றும் கேம்பிரியன் படிமங்கள் பற்றியும் விவரங்கள் அறிந்தோம்

வில்லியம் டெம்ஸ்கி ஒரு கணித ஆய்வாளர்.கணித முறையில் பரிணம செயலாக்கம் தவறு என நிரூபிக்க இயலுமா என்று ஆய்வு கட்டுரைகள் வெளியிட்டு வருகிறார்.

பரிணாம் கணித முறை எப்படி செய்ல்படுகிறது , எப்படி பயன்படுத்துவது என்பதை பற்றி இப்பதிவில் அறிவோம்.

வாழ்வில் சமூகம்,துறை சார்ந்த முடிவெடுக்கும் பிரச்சினைகள் சிக்கல்கள் உண்டு. சில பிரச்சினைகளை அனுபவம் கல்ந்தாலோசனை மூல்ம் முடிவெடுத்து தீர்க்க  முயல்கிறோம். அறிவியல்,தொழில் துறை சார்ந்த பல் பிரச்சினைகள் இப்படி மட்டும் தீர்க்க இயலாது.அவை மாதிர்களாக[mathematical models] கணித முடிவெடுக்கும் புதிர்களாக்[decision making problems or optimization] மாற்றப்ப்ட்டு கணிணி உதவியுடன் தீர்வுகள் கண்க்கிடப்படுகின்றன.

எ.கா

இரு ஊர்களுக்கிடையே இடையில் செல்லும் இருப்பு பாதை அமைக்க வேண்டும் எனில் அது பல விடயங்களில் முடிவெடுக்க வைக்கும்.

அதிக பட்சமாக முக்கிய ஊர்களை கடந்து செல்வது

அது குறைந்த பட்ச தூரமாக இருக்க வேண்டும்.

ஏற்கென்வே அங்குள்ள கட்டிடங்கள்,வயல்வெளிகள் போன்ற‌வற்றை பாதிக்காமல் இருக்க வேண்டும்.

புவியிய‌ல் ரீதியான சிக்கலகள்.,

பொருளாதாரம்

........

உண்மையில் இது குறித்தே பல பதிவுகள் எழுத இயலும் இங்கு நாம் முக்கியமாக் அ.வ[ID] கொள்கையாக்கம் பற்றியே கற்றுக் கொண்டு இருப்பதால் வாழ்வில் சந்திக்கும் பல பிரச்சினைகள் கணிதரீதியான் மாதிரிகளாக் வடிவமைக்கப்பட்டு தீர்க்க இயலும் என்பதை மட்டும் மனதில் இருத்தினால் போதுமானது.

இரண்டாம் உலக்ப்போரில் பிரிட்டன் வெல்வதற்கே இக்கணித முறை உதவியாக் இருந்தது என்றால் வியப்பாக இருக்கும்.[அது எப்படி என்று கேட்காதீர்கள்.அதற்கு ஒரு பதிவாகிவிடும்]

இது குறித்த விக்கிபிடியா படியுங்கள்.பின்னூட்டங்களில் சந்தேகங்களை தீர்க்க முயல்கிறேன்.

http://en.wikipedia.org/wiki/Operations_research

சரி ஒரு முடிவெடுக்கும் பிரச்சினயை கணித முடிவெடுக்கும் புதிராக மாற்றியாயிற்று.எப்படி பரிணாம் செயலாக்கம் கொண்டு தீர்க்க போகிறோம்?

முதலில் கணிதத்தின் ஒரு பிரிவான நுயுமெரிகல் முறையில் எப்படி தீர்க்கிறார்கள். என்பதை ஏற்கெனெவே பகுதி 8 ல் விவாதித்து இருந்தோம். அதன் இறுதியில் இப்படி முடித்து இருந்தோம்.

http://aatralarasau.blogspot.com/2012/02/7_09.html

நுயுமெரிகல் முறையில் முடிவெடுக்கும் புதிரை தீர்க்கும் போது இரு சிக்கல்கள் ஏற்படுவதை மீண்டும் அலசுவோம்.

1. நுயுமெரிக‌ல் முறையில் தீர்வின் தரம் தொடக்கப் புள்ளியை[starting solution] பொறுத்தே அமையும்.ஏனெனில் பல் தீர்வுகள் அமையும் வாய்ப்புள்ள கணிதப் புதிர்கள்தாம் மிகவும் கடினமான்வை.நுயுமெரிகல் முறையில் தொடக்கப் புள்ளிக்கு அருகில் உள்ள தீர்வே[local solution] கிடைக்கும்.கிடைத்த தீர்வை மேம்படுத்த முடியாது!!!!!!!!!.விடை தெரியாத புதிருக்கு மிக சிறந்த தீர்வுக்கு அருகில் உள்ள புள்ளியை எப்படி கண்டறிய முடியும்?

In numerical methods the converging(local) solution is depending on the initial starting solution.[எதை விதைக்கிறாயோ அதையே அறுப்பாய்!!!!!!!!!]

2. நுயுமெரிகல் முறையில் கணக்கிட்ட தீர்வை விட சிறந்த தீர்வு உள்ளத என்வோ அல்லது கிடைத்த் தீர்வுதான் மிக சிறந்த தீர்வு என் உறுதியாக் கூற இயலாது.கிடைத்த ஒரே தீர்வை வைத்துக் கொள்ள வேண்டியதுதான்.!!!!!

No converging solution can be assured  as global(best of all local)  solution[வல்லவனுக்கு வல்லவன் வையக்த்தில் உண்டு!!!!!!!].

ஒரே தீர்வே உள்ள கணிதப் புதிர்களுக்கு[convex problems] நுயுமெரிகல்முறையே சிறந்தது,எப்புள்ளியில் இருந்தும் அதே தீர்வுக்கு செல்லும் என்பதையும் அறிவது நல்லது.

அப்போது சகலவித சிக்க்லான கணித முடிவெடுக்கும் பிரச்சினைகளையும் மிகச் சரியாக‌ தீர்க்கும் சர்வ ரோஹ நிவாரணி முறை இதுவரை கண்டறியப்படவில்லையா? என்ப்தை முந்தைய பதிவுகளில் கேள்வியாக முன் வைத்தோம்.

 பரிணாம செய்லாக்க முறை[Evolutionary Algorithms] பல தீர்வுகள் உள்ள முடிவெடுக்கும் புதிர்களுக்கு[non convex problems]  தீர்வுகள் காணும் ஒரு முறையாகும்.நுயுமெரிசல் முறையின் எல்லைகளை கண்க்கில் கொண்டால் இது ஒரு அரிய [இயற்க்கையின்]வர பிரசாதமாகும்.இத்னை இது டார்வினின் பரிணாம் செயலாக்க முறையின் கணித மாதிரி ஆகும்.

பரிணாம் செயால்க்கம் பற்றி அனைவரும் நன்கு அறிவோம் என்றாலும் மீண்டும் விள்ங்குவோம்

1.  உயிரினக் குழுக்களில் சீரற்ற  சிறு மாற்றங்கள் தலைமுறை ரீதியில் பல்வேறு வகைகளை தோற்றுவிக்கிறது.

2.சூழலுக்கு பொருந்தும் மாற்றங்கள் கொண்ட உயிரினக் குழுக்கள் பெருகுகின்றன‌.மற்றவை அழிகின்றன்.

3.இவ்வாறே ஒரு செல் உயிரில் இருந்து அனைத்து உயிரினங்களும் ,தாவரங்களும் தோன்றின.

இதே போல்

பரிணாம் செயலாக்க முறை

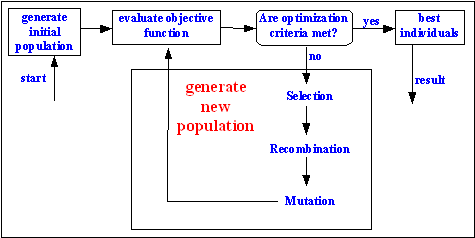
1. தொடக்க தீர்வுகள் சில சீரற்ற முறையில் எடுத்துக் கொள்ளப்படுகின்றன..Initial population chosen randomly.

இது முதல் தீர்வுக் குழு[initial population of solutions] எனப்படுகிறது.நுயுமெரிகல் முறையில் ஒரு தொடக்க தீர்வே[புள்ளி] எடுக்கப்படுகிறது என்பதை நினைவு கூறலாம்..Evolutionary algorithms are parallel search mechanisms.

2. முதல் தீர்வுக் குழுவின் ஒவ்வொரு தீர்வின் மீதும் மீது சில பரிணாம் செயல்பாடுகள் அமல்படுததப் படுகிறது.

அ) [இயற்கைத்]தேர்வு[selection]

இயற்கைத் தேர்வு என்றால் புதிருக்கு பொருந்தாத தவறான் தீர்வுகள் நீக்கப்பட்டு அந்த இடத்தில் ,பொருந்தும் நல்ல தீர்வுகள் பிரதியிடப்படுகின்றன்.

better solutions are chosen and replacing the bad solutions.

ஆ) கலப்பு[cross over or recombination]
இரு தீர்வுகள் கலக்கப்பட்டு புதிய [இரு] தீர்வுகள் உருவாக்கப்படுகின்றன்

இ) சீரற்ற சிறு மாற்றங்கள்[random mutations].

சில தீர்வுகளில் ஒரு மிக சிறிய மாற்றம் .எ.கா ஒரு 1% மதிப்பு அதிகரிப்பு அல்லது குறைப்பு செய்யலாம்.

3.இந்த‌ செயல் பாடுகளால் பயனால் தீர்வுக்குழு மாற்றம் அடைந்த தீர்வுக் குழு இரண்டாம் தீர்வுக் குழு ஆகிறது. இது ஒரு தலைமுறை[iteration] எனப்படுகிறது

4.இப்போதைய தீர்வுக் குழுவில் உள்ள சில தீர்வுகள் புதிருக்கு சரியான விடை தருகிறதா என பரிசோதிக்கப் படுகிறது.சோதனை வெற்றி என்றால் செயல்பாடு நிறுத்தப் படுகிரது.தோல்விஎன்றால் இரண்டாம் தீர்வின் மீது மீண்டும் இரண்டாம் நிலைக்கு சென்று அதே [அ,ஆ,இ]செயல்பாடுகள் என தொடர்கிறது.

முதல் தலைமுறை...இரண்டாம் தலைமுறை..,மூன்றாம்....நூறாம் தலைமுறை என தீர்வுகள் பரிணமிக்கின்றன. நமக்குத் தேவையான‌ தீர்வு இடையில் கிடைக்க்லாம் அலலது தேவையான தலைமுறை அளவு வைத்து கிடைக்கும் சிறந்த தீர்வை எடுக்க்லாம்.

பரிணாம் செயலாக்க முறைகள் ஒரு கடல்.கூடுமான்வரை எளிமைப்படுத்தி கூறவே விழைகிறேன்.

ஆகவே ஒரு சில தீர்வுகளை எடுத்து சில பரிணாம் மாற்றங்களை கணித ரீதியாக ஏற்படுத்தியது ஒரு தலைமுறை மாற்றமாகும்,குறிப்பிட்ட தலைமுறை கடந்த பின் உள்ள மாற்றம் அடைந்த தீர்வுகளில் சிறந்ததே கணித முடிவெடுக்கும் புதிருக்கு விடையாகும்.

இது மிகவும் எளிதான் செயல்கள் உள்ளதால் மென்பொருள்கள் [software] எழுதுவது மிக எளிது.எந்த சிக்க்லான கணித முடிவெடுக்கும் புதிரும் எளிதாக  பல தீர்வுகள் கண்டு பிடிக்கப் படுகிற‌து.

என்ன நண்பர்களே கொஞ்சம் புரிந்து,நிறைய குழப்பமாக் இருக்கும் என நம்புகிறேன்.முதலில் இதனை கற்கும் போது இது எப்படி மிகப் பெரிய கணித சிக்கலை தீர்க்க இயலும்.இதில் கணிதமே இலையே என்ற கேள்விகள் எனக்கும் வந்தது.ஆனால் தொடர்ந்த பயன்பாட்டின் மூலமே இதனை உணர முடிந்தது.

இதன் செயல்பாட்டுக்கு பல் நிரூபண்ங்கள்,சான்றுகள் அளிக்க முடியும்.கணிதத்தில் மட்டுமே பெரும்பாலும் 100% நிரூபணம் வழங்க முடியும்!!!!!!

அடுத்த பதிவில் ஒரு எடுத்துக் காட்டுடன் பரிணாம் செயலாக்க முறை எப்படி செயல் படுகிறது என்பதை விவாதித்து விள்ங்குவோம்!!!!!!!!!

நன்றி!!!!!!!!!!

http://en.wikipedia.org/wiki/Evolutionary_algorithm

http://www.geatbx.com/docu/algindex-01.html

Thanks Google,wikipidia