டெய்லர் தொடர் வரிசையின் நிரூபணம்

டெய்லர்  தொடர் வரிசையின் நிரூபணம்

வணக்கம் நண்பர்களே!

டெயலர் தொடர் வரிசை என்பது குறித்து உங்களில் பெரும்பானமையோர் அறிந்து இருக்கலாம.இத்தொடரில் அதற்கு நிரூபணம் தருவது எப்படி என்பதை எளிதாக கற்போம்.

சரி தொடர்வரிசை என்றால் என்ன?

ஒரு குறிபிட்ட எண்களோ , மாறிகளின் தொடர்போ[function of variables] ஒரு குறிப்பிட்ட சார்பு வீதத்தில் முன் செல்வது என கூறலாம், இப்பப்டிப்பட்ட கூட்டுத் தொடருக்கு பல சம்யங்களில்நிலையான எண்[finite number] அல்லது நிலையான மாறித் தொடர்பு[finite function] விடை உண்டு.

ஏன் பல சமயங்களில் என்று கூறுகிறோம்? சில சமயம் விடை முடிவிலி கிடைக்கலாம் என்பதற்காக அப்படி கூறினோம்.அப்போது முடிவிலி நிலையான எண் இல்லையா எனில் ,இதனை இல்லை என்று ஏற்கெனவே இப்பதிவில் கூறியுள்ளோம். நண்பர்கள் எப்போதும் ஒரு விடயத்தை மனதில் இருத்த வேண்டும்,ஒவ்வோரு விதிக்கும் எல்லைகள் உண்டு,எல்லைகளில் விதியை பொருத்துவதற்கு சில  மாறுதல்களை செய்ய வேண்டும்.

ஆகவெ முதலில் கற்கும் நண்பர்கள் எளிய வழியில் எந்த வித ஐயத்திற்கும் இடமில்லாத‌ விதி பொருந்தும் இடைவெளிகளில் நன்கு கற்று ஆராய்ந்து பிறகு விதியை சிறிது மாறுதலுடன் பயன்படுத்த வேண்டிய எல்லைகளுக்கு செல்வது நல்லது.  

இதன் எதிர் வினையும் உண்மையே ஒரு மாறித் தொடர்பு ,அல்லது நிலை எண்ணை முடிவிலி[அல்லது முடிவுறும்] கூட்டுத் தொடராக வரையறுக்க முடியும்.

எ.கா  

a)1,+2+,+3+4+5+,...+.n=n(n+1)/2

 b)

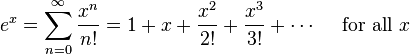
ஆகவே எளிதாக கூறினால் (பல) முடிவிலி தொடருக்கு சமமான நிலை எண் அல்லது ஒரு நிலையான் மாறித் தொடர்பு[function of variables] காண முடியும்.

இத எதிர்வினையும் உண்மையே

“பல‌ நிலையான‌ மாறித் தொடர்புகளை [finite functions] முடிவிலி தொடராக எழுத முடியும்”.

“A finite function can be expressed in terms of an infinite sum “

“Finite function=continuously differentiable”

நிலையான் மாறித் தொடர்பு எனில் தொடர்ச்சியாக சிறுமாற்ற விகிதம் கண்டறியத் தக்கது என பொருள் கொள்கிறோம்.

இப்பதிவில் எதிர்வினையை பற்றி மட்டுமே பார்க்கப்போகிறோம்.அப்போது முடிவிலி தொடர்களின் கூடுதலை நிலை எண் அல்லது மாறித் தொடர்பாக மாற்றுவது குறித்து கற்போம் என்கிறீர்களா. அதுவும் பிறகு முயற்சி செய்வோம்!

                                             

இப்போது எதிர்வினையான  ஒரு மாறித் தொடர்பை முடிவிலி தொடர்பாக எழுதுவதை கற்போம்.

என்ன கொஞ்சம் சிக்கலாக் இருப்பது போல் உள்ளதா!.சரி மிக மிக எளிமையாக் பேசுவோம்.

"ஒரு எதிர்கால சூழல் ஆனது கடந்தகால் நிகழ்கால சூழலை பொறுத்து இருக்கிறது"

இது என்ன மகா பெரிய தத்துவம்? இதுதான் அனைவருக்குமே தெரியுமே என்றால் அப்பாடா உங்களுக்கு புரியும் வகையில் பேசுவது நம்க்கு மகிழ்வே!.நாம் எழுதுவது உங்களுக்கு புரியவில்லை,அல்லது பிடிக்கவில்லை எனில் எழுதாமல் இருப்பதே நலம் என நினைக்கிறேன்.

ஆகவே புரியும் வகையில் மட்டுமே எளிமையாக் எப்போதும் எழுதுவோம் எனவே கூறுகிறோம்.

ஒரு இடத்தில் ஒரு மாறக்கூடிய  சூழலில் இருக்கிறோம்.அதில் இருந்து அருகே உள்ள இன்னொரு இடத்திற்கு செல்ல வேண்டும்.நாம் உள்ள இடத்தில் அறிந்த விவரங்களைக் கொண்டு அருகே உள்ள இடத்தின் சூழலை  அறிய முயல்வதுதான் இந்த தொடர்வரிசை கணித்தல் [prediction or extrapolation] என கூறலாம்.

இபோது நாம் இருக்கும் இடம் 3, இத்ற்கு முன் 2,அதற்கு முன்1 எனில் இத்தொடர் வரிசை எப்படி இருக்கும்?

1,2,3,4,5,6,7 என்று இருக்க வேண்டும்.இது சரிதான் என்றாலும் எப்போதும் சரியாக இருக்க வேண்டிய அவசியம் இல்லை.மொத்தம் மூன்று அள்வுகளை வைத்து இன்னும் மூன்று அள்வுகளை கணிப்பது என்பது பல நிகழ்வுகளில் சரியாக இருக்காது.அது பற்றி பிறகு பார்ப்போம்.

டெய்லர் தொடர் என்பது ஒரு  (முதல்) புள்ளியின் சூழல் குறித்த அளவைகள் கொண்டு  அறிந்து அருகே உள்ள  இன்னொரு (இரண்டாம்) புள்ளியின் சூழலை அள்ப்பது என கொள்ளலாம்.

f(x+a)=

 

If a=0

 

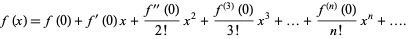
x=இப்போதைய (முதல்) புள்ளி

f(x)= (முதல்) புள்ளியின் சூழலின் அளவு

a=அருகாமை தூரம்

x+a= அருகாமை (இரண்டாம்)   புள்ளி

f(x+a)= அருகாமை  ((இரண்டாம்)  புள்ளியின் சூழலின் அளவு

f’(x)= முதல் சிறுமாற்ற விகிதம்[first derivative]

f²(x)= இரண்டாவது சிறுமாற்ற விகிதம்

..

.

.

f^N(x)= N வது சிறுமாற்ற விகிதம்

N=1,2,3,…ω

ஆகவே டெய்லர் தொடர்வரிசை என்பது முதல் புள்ளியின் அள்வு,சூழ,சூழலின் மாற்றங்களின் அடுக்குகளின் அள்வுகள் மூலம் அடுத்த புள்ளியின் சூழலின் அளவை கணிக்கிறோம்.

"ஆகவே எந்த ஒரு சிக்க்லான மாறித் தொடர்பையும் முடிவிலி எளிய மாறித் தொடர் அமைப்புகளாக் பிரிக்க இயலும்"

“Any function of higher order complexity can be expressed as a summation of simple power series”.

எங்கிருந்து எங்கே வருகிறோம் என புரிகிறதா?

சிறுமாற்ற விகிதம்[derivative] கண்டு பிடிக்கத் தெரிந்தால் கண்டறிந்து மதிப்புகளை பிரதியிட்டால் டெய்லர் தொடர் தேர்வு ரீதியாக முடிந்தது.ஆனால் அது என்ன என்பதையே அவதானிக்கிறோம்.

இப்போது நிரூபணத்திற்கு செல்வோம்

டெய்லர் தொடர்வரிசை அடுக்குத் தொடர் வரிசையின் ஒரு வகை ஆகும். அடுக்குத் தொடர் வரிசையின் குணகங்களை(coefficients) கண்டறிந்தால் டெய்லர் தொடர்வரிசை தயார் ஆகிவிடும்.

அடுக்குத் தொடர் வரிசை என்றால் என்ன எந்த ஒரு சிக்கலான மாறித் தொடர்பையும் முடிவிலி எளிய மாறி அடுக்குகளின் கூட்டுத் தொடர் வரிசையாக் கூற முடியும்.

a0,a1,a2,… கண்டறிந்தால் டெயலர் தொடருக்கு நிரூபணம் ஆகிவிடும்.

இப்போது x=c என பிரதியிடுவோம்.

f(c)=a₀

இபோது முதல் சிறுமாற்ற விகிதம் கண்டு பிடித்து மீண்டும் x=c என பிரதியிட்டால் a₁ ன் மதிப்பு கிடைக்கும்

f^’(x)=0+a₁+2*a_2*(x-c)+3a₃(x-c)²+….+n.a_n.(x-c)(^n-1)+….

இப்போது x=c என பிரதியிடுவோம்.

f¹[c]=a₁

…..

f ²[c]/(2!)=a2

….

…

f ⁿ[c]/(n!)=a_n

இந்த மதிப்புகளை அடுக்குத் தொடர் வரிசையில் பிரதியிட்டால் டெய்லர் தொடர் கிடைக்கும்.

f(x+a)=

 

If a=0 என பிரதியிட்டால் மெக்லாரின் தொடர்வரிசை கிடைக்கும்.

 

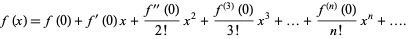
ஆகவே டெய்லர் தொடர்வரிசை நிரூபிக்கப்பட்டது.

இப்போது விதண்டாவாதம்

சரி அடுக்குத் தொடர் வரிசையில் இருந்து டெயலர்,மெக்லாரின் தொடர்வரிசை கண்டு பிடித்தோம் இதை எப்படி நிரூபணமாக் எடுக்க முடியும்?. இது அடுக்குத் தொடர்வரிசை எந்த அளவு உண்மையோ ,டெய்லர் தொடர்வரிசையும் அந்த அளவே உண்மையாக் இருக்க முடியும்???????????.

சரியான் கருத்து எனினும் அடுக்குத் தொடருக்கு இன்னொரு அடிப்படை இப்படியே ஒன்று[1] என்ற எண்ணின் வரையறை வரை செல்லும்.அடுக்குத் தொடரின் நிரூபண்ம் கொஞ்சம் கடினம்!!!!!!!!!!!!!.

கடினம் என்ற சொல்லை அதற்கு இன்னும் பல் அடிப்படைத் தேற்றங்கள் தேவைப்படும் என்ற பொருளிலேயே கூறுகிறோம்.தொடர்சியான் எளிய அமைப்புகளின் கூட்டமைப்பு சிக்க்லான அமைப்பை உருவாக்கும் என்பதையும் அடுக்குத் தொடர் வர்சையில் இருந்து அறியலாம்.

இங்கே அறிய விரும்புபவர்கள் அறியலாம்.

http://www.proofwiki.org/wiki/Derivative_of_Complex_Power_Series/Proof_1

ஆகவே முதலில் அடுக்குத் தொடர்வரிசை நிரூபண்ம்  எங்களுக்கு புரியும் வரை டெய்லர் நிரூபண்மும் செல்லாது செல்லாது!,என எதிர் பதிவு இட விரும்பும் நண்பர்கள் இட வலியுறுத்துகிறோம்.

கணிதத்தில் மட்டுமே மிக சரியான நிரூபணம் தர முடியும் என்றாலும் அது சாமான்யனுக்கும் புரியும் வரையில் எளிமைப்படுத்துவது என்பதற்கு கடும் ,தொடர் உழைப்பு தேவைப்படும்.அதில் நாம் ஒரு துரும்பை எடுத்து விளக்க  முயற்சிக்கிறோம் அவ்வளவுதான்!.

எல்லாவற்றுக்கும் அடிப்படை ஒன்றே,அந்த அடிப்படையில் இருந்தே அனைத்து அறிவியலும் கிளைத்து தழைத்தன என்பதை அறியாமல், எதையும்  பிற விளக்கங்கள் சாராமல் அறிய இயலாது என்பதை அறியாமல்  எழும் கேள்விகளை புறக்கணிப்போம்.கற்றல் என்னும் தொடர் தேடலை தொடர்வோம்.

இப்பதிவின் சாரம்

1.ஒரு (நிலையான) கடின்மான (சிக்க்லான) மாறித் தொடர்புக்கு சமமான  எளிமையான் மாறி அடுக்கு தொடர்வரிசை உண்டு. 

2.அடுக்குத் தொடர்வரிசை என்பதை இரு வகைகள்தான் டெய்லர்,மெக்லாரின் தொடர் வரிசைகள்.அடுக்குத் தொடர்வரிசையில் சில கணித செயல்க‌ள் + பிரதியிடுதல் மூலம் டெய்லர்,மெக்லாரின் தொடர் வருவிக்க முடியும்.

3.இவை மாறித் தொடர்பு எளிமைப்படுத்தல்[function approximation],எதிர்(கடந்த)கால நிகழ்வு கணித்தல்[prediction or extrapolation] போன்ற விடய‌ங்களுக்கு பயன்படுகின்றன.