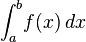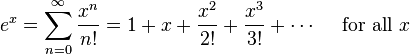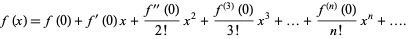நித்தியானந்தாவின் மதுரை ஆதீன‌ பதவி ஏற்பு காணொளி

நித்தியானந்தா என்னும் ஆன்மீக பிரச்சாரகர் சர்ச்சைக்குறிய வழக்கில் குற்றம் சாட்டப்பட்டு  கைதாகி புகழ் பெற்றவர் என்பது அனைவரும் அறிந்ததே. இப்போது எதிர்கால மதுரை ஆதினமாக பதவி ஏற்கிறார் என்பது செய்தியை அதிர்ச்சியும் ஆச்சர்யமும் கொண்டே கேட்க வெண்டி உள்ளது.

அரசியலிலும் ஆன்மீகத்திலும் என்ன வேண்டுமானாலும் நடக்கும் என்பது நிரூபணம் ஆகிவிட்டது.

இதை என்னைசொல்வது என்றே தெரியாததால் பதவி ஏற்பு குறித்த காணொளிகளை மட்டும் வழங்குகிறோம்.பிற மாநில மொழி காணொளிகளை சேர்த்து வழங்குகிறோம்.

சகோதர சகோதரிகளே ஆன்மீக(மத) பிரச்சாரகர்களிடம் எச்சரிக்கையாக் இருக்கவும்  வேண்டுகோள் விடுக்கிறோம்.

நன்றி

In English

Kannada

Telugu

கருப்பு ஆற்றல்& கருப்பு பொருள்[Dark Matter&Dark Energy] என்பது கட்டுக் கதை ஆகுமா?

இப்போதைய  பேரண்டவியலில் அறிவியலில் ஏற்றுக் கொள்ள்ப்பட்ட  கொள்கையாக்கம் "அதிகரிக்கும் வேகத்தில் விரிவடையும் பிரபஞ்சம்" என்பதுதான். பேரண்டத்தின் விரிவடையும் வேகம் அதிகர்ப்புக்கு காரணம் அதில் உள்ள கருப்பு பொருள் என்னும் கொள்கையாக்க விளக்கம்,ஆய்வுகளுக்கு 2011 இயற்பியல் நோபெல் பரிசும் வழங்கப்பட்டது.

சரி கருப்பு ஆற்றல்& கருப்பு பொருள் என்றால் என்ன?

http://science.nasa.gov/astrophysics/focus-areas/what-is-dark-energy/

மேலே குறிப்பிட்ட சுட்டியின் தமிழாக்கம் அளிக்கிறோம். 90களின் தொடக்கத்தில் பேரண்டம் விரிவடைவது குறித்து அறிவியலில் ஒருமித்த  கருத்தாக்கம் ஏற்கப்பட்டது. அது சார்ந்து இந்த பேரண்டம் எவ்வளவு காலம் விரிவடையும்?அதற்கு ஒரு எல்லை உண்டா  என்பதும் விடையளிக்க முற்பட்டனர்.

இரு வாய்ப்புகள்

1.ஒரு அள்வு விரிவாக்கதின் பின் பேரண்டத்தின் ஆற்ற‌ல் அடர்த்தி அதனை மீண்டும் சுருங்க வைக்கும் அள்வு இருக்க்லாம்.

அல்லது

2.அதன் ஆற்றல் அடர்த்தி மிக குறைவாக இருந்து பேரண்டம் எப்போதும் விரிவடைந்து   கொண்டே இருக்கலாம்.

இரண்டு வாய்ப்புகளிலும் கால்ப்போக்கில் விரிவடையும் வேகம் ஈர்ப்பு விசையால் குறைய வேண்டும் என்பது கணிப்பு. ஆனால் விரிவடையும் வேகம் குறைவாதாக் பரிசோதனை அள்வுகளில் தெரியவில்லை. இப்பேரண்டம் முழுதும் பருப்பொருள்[matter] உள்ளது ஈர்ப்பு விசை என்பது அனைத்தையும் இழுக்கிறது. ஈர்ப்பு விசை என்பது ஒன்றை நோக்கிய‌ மற்றொன்றின் பரஸ்பர இழுப்பு மட்டுமே இது விலக்கு விசை அல்ல என்பதை புரியவேண்டும்.

1998ல் ஹூபில் தொலை நோக்கி மூலம் நடத்தப்பட்ட ஆய்வு அள்வுகள் தூரத்தில் உள்ள வெளித் திரள்களின் நடசத்திரவெடிப்பு(சூப்பர் நோவா)களின் விலகும் வேகத்தை கண்க்கிட்டது.

இப்போதைய வேகத்தை விட கடந்த காலத்தில் பேரண்டம் குறைவான் வேகத்தில் விரிவடைந்தது என்பதுதான் இந்த பரிசோதனையின் முடிவு.

இந்த விரிவடைதலின் வேக அதிகரிப்பை எப்படி விள்க்குவதென்ற முயற்சியில் மூன்று கருதுகோள்களை முன் வைக்கின்றனர்.

1.ஐன்டினின் ஈர்ப்புவிசை மற்றும் அண்டவியல் மாறிலி சார்ந்த விளக்கம்.

2. பேரண்டம் முழுதும் ஒரு அறியா திரவம் போன்ற பருப்பொருள் நிறைந்து உள்ளது.

3. ஐன்ஸ்டினின் ஈர்ப்பு விசைக் கொள்கை தவறு மாற்றுக் கொள்கை தேவை.

இதன் விடை இன்னும் சரியாக அறியப்படவில்லை எனினும் இப்படி விரிவடையும் வேகம் அதிகரிப்பின் காரணம் எது என்ற கேள்விக்கு விடையாக  கருப்பு ஆற்றல் என வரையறை செய்தனர்.

கருப்பு ஆற்றல்

பேண்டத்தின் விரிவாக்கத்தின் வேகத்தை அதிகரிக்கும் ஒருவகை ஆற்றல் என்பதே இதன் வரையறுப்பு.கட‌வுளை அறிய முடியுமா என்றால் அறிய முடியாததுதான் கடவுள் என்ற  குழப்பமான‌ மதவாதிகள் விளக்கம் போல் உள்ளதா.மன்னிக்கவும் அறிவியலின் வரையறுப்பு இதுதான்.

அறிவியலின் வரையறுப்பை நினைவு கூற வேண்டுகிறேன். இயற்கையின் நிகழ்வுகளை விளக்குவதே அறிவியல்.இயற்கை நிகழ்வுகளை அதன் காரணிகளாக  பகுத்து ,அவற்றுக்கு இடையே தொடர்புகளை நிறுவுவதும் ,அதன் மூலம் கணிக்கும் விடயங்களை ஆய்வுரீதியாக் உறுதிப்படுத்துவதும் இதன் அங்கங்கள் என அனைவரும் அறிவோம்.

இங்கு இயற்கை நிகழ்வான‌ பேரண்ட விரிவடைவின் வேகம் அதிகரித்தல் உறுதி செய்யப்பட்ட உண்மை என்வே கொள்ளலாம்.

பேரண்டத்தின் விரிவடையும் வேகம் குறையாமல் அதிகரிப்பதின் காரணியாக  கருப்பு ஆற்றல் என்ற ஒன்று இருக்க வேண்டும் என்ற கருது கோளின் படி இந்நிகழ்வு விளக்க ஏதுவாக உள்ளது.எனினும் இதன் மூலம் கணிக்கபடும் விடயங்கள் ஆய்வு ரீதியாக் உறுதி செய்யப்பட்டால் மட்டுமே இது முழுமையாக் ஏற்கப்படும்.

பேரண்டத்தில் 70% கருப்பு ஆற்றலும் 25% கருப்பு பொருளும் இருப்பதாக கணிக்கப்பட்டு உள்ளது.மீதம் உள்ள 5% தான் அனைத்து வெளித்திரள்களும்[galaxy],விண்மீன்கள்[stars],கோள்கள் சேர்ந்த அளவு.அதில் பூமி ஒரு தூசி.

ஆகவே நாம் அறிந்த பேரண்டம் மிக சிறிய அளவு மட்டுமே.சில அறிவியலாளர்கள் இந்த கருப்பு ஆற்றலை வெற்றிடத்தின் ஒரு தன்மையாகவும் வரையறுக்கிறார்கள். வெற்றிடம் என்பது உண்மையில் சூன்யம் அல்ல என்ற் கருத்தை முதலில் வெளியிட்டவர் ஐன்ஸ்டின். வெற்றிடம் அதன் அளவை அதிகரிக்க முடியும் என்பதை அதன் தன்மையாக வரையறுத்தார் ஐன்ஸ்டின்

அதாவது அறிவியலில் உள்ள கருதுகோள்கள் பெரும்பாலானவை தத்துவம் போலவே இருக்கும். ஐன்ஸ்டினின் ஈர்ப்பு விதி கொள்கையாக்கத்தில் அண்டவியல் மாறிலி[cosmological constant]  என்று ஒன்று உண்டு.இது பற்றி ஒரு தனிப் பதிவு இட்டு விடுவோம்.

வெற்றிடத்தில் ஆற்ற‌லும் இருக்கும் என்பது ஐன்ஸ்டினின் இன்னொரு கணிப்பு.

ஐன்ஸ்டினின்  முதல் கணிப்பின்படி வெற்றிடம் விரிவடையும் போது அதன் ஆற்றலும் அதிகம் தோன்றுகிறது.இந்த ஆற்ற‌ல் வெற்றிடத்தை அதிகரிக்கும் வேகத்தில் விரிக்க ,விரிவடைதலின் எல்லை அண்டவியல் மாறிலியின் அள‌வின் மூலம் தீர்மானிக்கப்படுகிறது.

இந்த கருப்பு ஆற்றலின் இன்னொரு விள்க்கம் குவாண்டம் பருப்பொருள் கொள்கையாக்கதின் அடிப்படையில் ஆனது.அதாவது வெற்றிடம் என்பதில் பல பருப்பொருள்கள் தோன்றுவதும்,மறைவதும் மிக இயல்பான விடயம்.அப்ப்டி உள்ள வெற்றிடத்திற்கும் கணிக்கப்பட்டகருப்பு ஆற்றலுக்கும் தொடர்பினை கண்க்கிட்டு பார்த்த போது தவறு அதிகம் வந்ததால் இதனை கைவிட்டு விட்டார்கள்.

இன்னொரு விளக்கமான் ஐன்ஸ்டினின் ஈர்ப்பு விசை கொள்கை முற்று முழுதும் த்வறு இதற்கு மாற்றுக் கொள்கை கண்டுபிடிக்கப்படவேண்டும்.இது பேரண்டம் விரிவடைகிறதா என்பதையே சந்தேகத்திற்கு உள்ளாக்கும். ஐன்ஸ்டினின் ஈர்ப்பு விசை கொள்கை சூரிய குடுப்பம்,வெளித்திரள் ஆகியற்றின் இயக்கங்களை மிக சரியாக் விள்க்குவதால் மாற்றுக் கொள்கைக்கு இந்த இயக்கங்களையும் விள்க்கி ,விரிவடைதலின் வேகம் அதிகரித்தலையும் விள்க்க வேண்டிய தேவையும் உள்ளது.

ஆகவே கருப்பு ஆற்றல் என்பது வெற்றிடத்தின் தன்மையா? ,ஒரு அறியா பருப்பொருளா? அல்லது மாற்று ஈர்ப்பு விசைக் கொள்கை தேவையா?  என்பதில் ஏதேனும் ஒன்றின் மூலம் விடையளிக்கப்படலாம்.இப்போதைக்கு விடை தெரியா கேள்வி.

கருப்பு பொருள்

இதை பற்றியும் ஒன்றும் தெரியாது.பேரண்டத்தில் பார்க்க முடியாத பல பருப் பொருள்கள் உள்ளன.நமது பேரண்டத்தில் 25% கருப்பு பொருள் உள்ளது என்பதை ஏற்கென்வே குறிப்பிட்டோம்.

கருப்பு பொருள் என்னவாக இருக்க முடியும் என்பதைவிட என்னவாக இருக்கமுடியாது என்பதை அறிவியல் தெளிவாகவே வரையறுக்கிறது.

[நாமும் இதே போல் கடவுள் என்னவாக இருக்க முடியும் என்பதைவிட என்னவாக இருக்கமுடியாது அடித்துக் கூற இயலும்.]

இப்படி கருப்பு பொருள்  என்னவாக் இருக்க முடியாது என்ற வரையறைகள்

1. விண்மீன்கள்,கோள்கள் போல் கண்ணுக்கு தெரிவது இல்லை.இப்படி கண்னுக்கு தெரியாத பொருள்கள் 25% இருந்தாகவேண்டும் என பரிசோதனைகள் கூறுகின்றன.

2.கண்னுக்கு தெரியாத, ஆனால் பரிசோதனையில் கண்டுபிடிக்கக்கூடிய பேரியான் போன்ற அணு துணை துகள்களால் ஆன பருப்பொருள்களும் அல்ல.இவைகளை வெப்பக் கதிவீச்சு உள்வாங்குதலின் மூலம் கண்டறிய முடியும்

3.கருப்பு பொருள் எதிர் பருப்பொருள் அல்ல. பருப்பொருள் எதிர் பருப்பொருளுடன் இணைந்தால் காமா கதிர்கள் வெளிப்படுவதை உணர முடியும்.

4.இது கருந்துளையும் அல்ல.கருந்துளைகளை பரிசோதனையின் மூலம் கண்டறிய முடியும்.எப்படி எனில் இங்கே பார்த்துக் கொள்ளுங்கள்.

http://en.wikipedia.org/wiki/Gravitational_lens

இப்படி ஒளியை ஈர்த்து  வளையச்செய்யும் தன்மை உடைய இந்த நான்குவகை தன்மை பொருள்களிலும் அடங்காத வகைதான் கருப்பு பொருள்.இப்படிப்பட்ட பொருள்கள் 25% பேரண்டத்தில் இருக்கவேண்டும் என்பதே கணிப்பு .

மேலே சொன்னது எதுவுமே புரியவில்லை என்றாலும் கவலையில்லை.நம் பாணி ஒரு வரி விள்க்கம்!

1.பேராண்டம் விரிவடைதலின் வேகம் அதிகரிப்பின் காரணியாக வரையறுக்கப்படுவது கருப்பு ஆற்றல் இது பேரண்டத்தில் 70% உள்ளது.

2.பரிசோதனைகளால் அறியப்படாத ஈர்ப்பு விசையின் காரணி கருப்பு பொருள்.இது பேரண்டத்தில் 25% உள்ளது.

இதைதான் கட்டுக் கதை என்று குறிப்பிடுகிறீர்களா என்றால் இல்லை.கடந்த சில வாரங்களுக்கு முந்தைய ஒரு செய்தி குறித்தே பதிவு எழுத விரும்பினேன்.நாம் ஒரு பதிவு எழுதும் போது அது முழுமையாக இருக்க வேண்டும் என்பதல் கருப்பு ஆற்ற‌ல்& கருப்பு பொருள் பற்றியும் எளிமையாக விள்க்க வேண்டியதாயிற்று.

சரி செய்திக்கு செல்வோம்.

http://www.sciencedaily.com/releases/2012/04/120418111923.htm

Serious Blow to Dark Matter Theories? New Study Finds Mysterious Lack of Dark Matter in Sun's Neighborhood

 

ஐரோப்பிய லா சில்லா சதர்ன் ஆயவக்த்தில்[European Southern Observatory's La Silla Observatory] உள்ள சக்தி வாய்ந்த MPG/ESO 2.2-metre  தொலைநோக்கி  மூலம நடத்தப்பட்ட சில ஆய்வுகளின் முடிவுகள் வெளியிடப்பட்டன. இதில் 400க்கும் மேற்பட்ட 13,000 ஒளிவருடங்கள் தூரம் உள்ள விண்மீன்களின் இயக்கங்கள் கண்டறியப்பட்டன. இந்த புதிய தகவல்கள் அடிப்படையில் சூரியனுக்கு அருகில் உள்ள இடத்தின் எடை ,க‌ன பரிமாணத்தின் அடிப்படையில் கண்டறியப்பட்டது.இந்த கன்பரிமாணமானது இதுவரை எடுத்துக் கொள்ளப்பட்ட அள்வைகள் போல் 4 மடங்கு ஆகும்.

இபோது அறியப்பட்ட பருப்பொருள்களின விண்மீன்கள், காற்று,தூசி முதலியைவை தவிர்த்த எடை கருப்பு பொருளின் எடையாக இருக்கும் என்பதே கருத்தாக்கம்.

"The amount of mass that we derive matches very well with what we see -- stars, dust and gas -- in the region around the Sun," says team leader Christian Moni Bidin (Departamento de Astronomía, Universidad de Concepción, Chile). 

ஆனால் மிச்சம் மீதி எடை மிக மிக குறைவு.அதாவது இல்லை என்றே கூறிவிடலாம்.இதுதான் அங்கே நிகழ்ந்தது.

சரி இத்னால் கருப்பு பொருள் என்பதே இல்லை என்று கூற முடியாது என்றாலும், சூரியனுக்கு அருகில் உள்ள அளக்கப்பட்ட இடத்தில் இல்லை என்ப்து உறுதி.கருப்பு பொருள் பூமியை ஊடுருவி செல்கிறது என்ற கருதுகோளின் அடிப்படையிலும் பல சுரங்க ஆய்வகங்கள் நிறுவப்ப்ட்டு அத்னை உண்ர முடியுமா எனனும் ஆய்வுகளிலும் இதுவரை எந்த முன்னேற்றமும் இல்லை.

சரி இதெல்லாம் 5% பேரண்டத்தில் ஒரு சிறு பகுதியில்தானே ஆய்வு செய்து இருக்கிறோம்.இந்த 5% தாண்டி ஆய்வுகள் நிகழும் போது மட்டுமே உறுதியாக கூற இயலும் என்றாலும் இதிலும் கருப்பு பொருள்&ஆற்ற‌ல் கொஞ்சமாவது கண்டறிந்தால் மட்டுமே இது இருப்பதன் சாத்தியம் உண்டு.

5% அறியப்பட்ட பேரண்டத்திலும் கருப்பு பொருள் அல்லது கருப்பு ஆற்றல் கொஞ்சமாவது உணரப்பட முடியும் என்ற தேடல் தொடர்கிறது.

காணொளியில் கருப்பு பொருள் ,கருப்பு ஆற்ற‌ல் பற்றி அருமையாக விளக்குகிறார்கள் கண்டு களியுங்கள்!.

நன்றி


Thanks google

தொகை நுண்கணிதம்[Integral Calculus] என்றால் என்ன? Part 1

வணக்கம் நண்பர்களே!

சில அறிவியல்,கணித தலைப்புகளை எளிமைப்படுத்திய விளக்கம் அளிப்பதின் தொடர்ச்சியாக  இப்பதிவில் தொகை நுண்கணிதம் என்பதை பற்றி பார்ப்போம்.ஏற்கென‌வே சிறுமாற்ற விகிதம் (derivative அல்லது வகைக்கெழு பற்றி முந்தைய பதிவில் பார்த்தோம்.

சிறுமாற்ற விகிதத்தின் எதிர்செயல்தான் தொகை நுண்கணிதம் ஆகும்.சிறுமாற்ற விகிதம் எனில் ஒரு மாறியின் சிறுமாறுதலுக்கு மாறித் தொடர்பு [function] எப்படி மாறுகிறது என்பதன் விகிதம் என்பதை அங்கு பார்த்தோம்.

It is the ratio of function’s change with respect to the small change in (a) variable(s).

இப்பதிவில் தொகை நுண்கணிதம் என்னும் சொல்லின் விள்க்கம்,சில பயன்பாடுகள் எளிய தமிழில் அறிவோம்.

தொகை நுண்கணிதம் என்று மிகசரியாக தமிழாக்கம் செய்த அறிஞருக்கு நம் நன்றி.

சரி  தொகை என்றால் என்ன ?

சரியான தமிழில்  amount என்று தமிழர்கள் அனைவருக்கும் தெரியும்!.

தொகை என்னும் சொல்லுக்கு மொத்த அளவு என விளங்கலாம்.

சரி முதலில் கூட்டல் என்பதை புரிந்து கொள்வோம்! .

என்ன சகோ தொகை நுண்கணிதம் பற்றி அதி அற்புதமாக் விளக்கப் போகிறீர்கள் என வந்தால கூட்டல் என்று சொல்லிக் கொண்டு,அதுதான்  தெரியுமே! என்கிறீர்களா!.

உலகில் உள்ள அனைத்து விடயங்களுமே எளிமையாக பிரித்து அறியப்படவும் எவராலும் உண்ரப்பட்வும் முடியும் என்ற கொள்கை உடையவர்கள் நாம்.அதி அற்புதம்,எங்கும் காணா உன்னதம், ஈடு இணையற்றது. போன்ற விடயங்களை நாம் ஏற‌பது இல்லை.

கணிதத்தில் அனைத்துமே கூட்டலே!

கழித்தல் என்பது திசை மாறிய கூட்டல்

4 –‍ 2 =4+(-2)=2‍‍

பெருக்கல் என்பது தொடர் கூட்டல்

4X2=2+2+2+2+2=8

வகுத்தல் என்பதும் திசைமாறிய தொடர் கூட்டல்

8/2= the no of ‘2’s can be subtracted continuously without becoming a negative number

8+(-2-2-2-2)=0 so 4

கூட்டலில் பலவகை உண்டு.இபோது நாம் பார்த்த பெருக்கல் ,மற்றும் வகுத்தல் ஆகியவை இருபரிமாண கூட்டலுக்கு எடுத்துக் காட்டு ஆகும்.

ஒரு எண்ணை இன்னொரு எண்ணுடன் எத்தனை முறை கூட்டுகிறோம் என்பதுதான் பெருக்கல். இதுதான் இருபரிமாண கூட்டல் .

பரப்பளவு என்பது பெரும்பாலும் பெருக்கலுக்கு பயன்பாடுள்ள‌ ஒரு செயலாகும். ப்ரப்பளவு என்றால் ஒரு அலகு பக்க அளவு உடைய சதுரங்கள் குறிப்பிட்ட பரப்புக்குள் எத்தனை இருக்கிறது என்பதை கண்டறிவதாகும்.

அறிவியலில் அனைத்துமே ஒரு நன்கு வரையறுக்கப்பட்ட அலகு போல் அளக்க வேண்டியதில் எத்தனை இருக்கிறது [relative] என்பதை கூறுவது மட்டுமே என்பதை நினைவுறுத்த வேண்டுகிறேன்.

சரி தொகை என்று ஆரம்பித்து கூட்டலில் வந்து நன்கு விள்ங்கி விட்டொம்.நுண்கணிதம் என்றால் சிறுமாற்ற விகிதத்தின் அடிப்படையில் தொடர்புகளை உருவாக்குதல்,கணித்தல் என கூறலாம்.

சரி தொகை நுன்கணிதம் என்றால் என்ன?

முதலில் ஒரு கதை சொல்கிறேன்

ஒரு பேராசை கொண்ட மனிதன் இருந்தான். ஒரு இடத்தில் நிலம் குறைந்த விலைக்கு  விற்பதாக தக்வல் அறிந்து அங்கு சென்றான்.என்ன விலை நிலம் என்றான்.அதற்கு அவர்கள் ஒரு நாள் நிலம் 1 இலட்சம் ரூபாய் என்றார்கள்.நம் பேராசை  நண்பருக்கு ஒன்றும் புரியவில்லை. அது என்ன ஒருநாள் நிலம், முதல்வன் பட ஒரு நாள் முதல்வர் மாதிரியா என அப்பாவியாக கேடக,அதற்கு அவர்கள் எங்களிடம் ஒரு இலட்சம் ரூபாய் கொடுத்து விட்டு அதிகாலை சூரியன் உதிப்பில் இருந்து ஓட ஆரம்பித்து மறையும் முன் எவ்வள்வு பரப்பு உன்னால சுற்றி தொடங்கிய இடத்திற்கு வர முடியுமோ அவ்வளவும் உனக்குத்தான் என்றார்கள்..ஆனால மறையும் முன் தொடங்கிய இடம் வர வேண்டும்.ஓடும் போது சில கொடிகளை நட்டு ஓடும் பாதையை அடையாளம் காட்ட வேண்டும் என்றார்கள்.

ஆஹா என்ன அபாரமான் விடயம்.உடனே கொடுத்தார் ஒரு இலட்சம்.அடுத்த நாள் அதிகாலையில் அனைவரிடமும் சொல்லி தொடங்கும் இடத்தை நன்கு குறித்து ஓடத் தொடங்கினார். நண்பர் நிலப் பிரியன். ஒரு பெரிய சதுரம் போடுவது அவர் எண்ணம். காலை 6 மணி முதல் சாயங்காலம் 6 மணி வரை 12 மணி நேரம்.ஆகவே கிழக்கில் மூன்றுமணி,பிறகு வடக்கு,மேற்கு,தெற்கு என தலா மூன்றுமணி நேரம் ஓடி தொடங்கிய இடத்திற்கே வருவது அவர் நோக்கம்.

ஓடினார் கிழக்கில் மூன்று மணி நேரம் பிறகு கொடியை நட்டார்.திரும்பினார் வடக்கே மூன்று மணி நேரம். கொடியை நட்டார்.காலகள் தடுமாறியது.தாகம் பசி எடுத்தது.இருந்த தண்ணீர் மட்டும் குடித்தார்.பேசாமல் குறுக்கே சென்று தொடங்கிய இடத்தை அடையலாம அப்படி எனில் முக்கோணம் போல் ஆகிவிடும்,நாம் நினைத்ததில் பாதியா எனக்கு முழுதும் வேண்டும் என மேற்கே முக்கி முனகி மூன்று மணி நேரம் ஓடினார்.ஓடி ஓடி மயக்கம் வந்து விட்டது. மூன்று மணி நேரம் ஆனதும் திருப்பி தெற்கே அவரால் நடக்கவே முடியவில்லை.உயிரை கையில் பிடித்து ஓடினார்.சூரியன் மறைவது போல் இருந்தால் மிக வேகமாக சக்தியெல்லாம் திரட்டி ஓடி தொடங்கும் இடம் தெரியும் அளவு வந்து விட்டார்.

இன்னும் கொஞ்ச தூரம் என்னும் போது மயங்கி விழுந்தார்.அனைவரும் வந்து பார்த்த போது அவர் உயிருடன் இல்லை.

அவருக்கு கிடைத்த‌து 6 க்கு 3 அடி நிலம் மட்டுமே!

ஆமா இந்த கதை எதுக்கு என்கிறீர்களா.பரப்பளவு, பயணித்த தூரமும் வருகிற‌து அல்லவா அதுக்குத்தான்!

என்ன சகோ இப்படி ஓ பி அடிக்கிறீங்க நீங்கள் என்ன ஆசிரியரா என்றால் நாம் என்றுமே மாண்வன் என்றே பணிவுடன் அடகத்துடன் கூறுகிறோம்.

சரி சகோ போதும் தொகை நுண்கணிதம் செல்ல‌லாம என்றால் சரி செல்வோம்.

"தொகை நுண்கணிதம் என்பது ஒரு மாறித் தொடர்பு, அதன் எல்லைகளால்  அடைபடும் பரப்பளவு கணிப்பது ஆகும்" 

Integral is defined informally to be the area of the region in the xy-plane bounded by the graph of f, the x-axis, and the vertical lines x = a and x = b, such that areas above the axis add to the total, and the area below the x axis subtract from the total.

இப்ப சொல்லுங்க சொன்ன கதை,விவரங்களுக்கு தொடர்பு இருக்கிறதா இல்லையா!

இக்கதை சொல்லும் நீதி என்ன ?

"பயணிக்கும் பாதை சரியான இடத்திற்கு கொண்டு செல்லுமா என்பதை அறிவதே சிறப்பு"

இப்போது ஒரு கேள்வி கதையில் நண்பர் நிலப்பிரியன் சதுரம் அமைக்க ஓடினார். 

தூரம் குறைவாக ஓடி அதிக பரப்பு அடைய வேண்டுமெனில் எப்படி ஓட வேண்டும்?. அதாவது பயணிக்கும் பாதை எந்த வடிவில் இருக்க வேண்டும்?.

சிந்திக்க மாட்டீர்களா!!!!!!!! 

அது என்னமோ, என்ன மாயமோ தெரியலை இந்த பதிவு முழுதும் கதை கதையாக  வருகிறது. ஆகவே அடுத்த பதிவில் நாம் தொகை நுண்கணிதம் உண்மையிலேயே கற்போம்.

நன்றி

இதுவே இந்தியா!: வெள்ளிப் பனிமலையின் மீதுலாவும் உயிரினங்கள்

 

வணக்கம் நண்பர்களே!

இமயமலை எனது நமது வட‌ எல்லைப்பகுதி என்பது அனைவரும் அறிந்த விடயமே!. மகாகவி பாரதியாரும் வெள்ளிப் பனிமலையின் மீதுலாவுவோம் என்று பாடினாலும் அதை உண்மையாக்குவது மனிதர்கள் அல்ல!!!!!!!!!!.

அச்சூழலிலும் அங்கு வாழும் சில விலங்குகளே.இந்திய துணைக்கண்டம் 70 மில்லியன் ஆண்டுகளுக்கு ஆப்பிரிக்கவில் இருந்து பிரிந்து வந்து [15 cms per year] ஆசியாவின் மீது மோதிய போது இமயமலை ஏற்பட்டதாக அறிவியல் கூறுகிறது.

சரி காணொளி தயாரித்தது நமக்கு நன்கு அறிமுகமான தலை டேவிட் அட்டன்பரோதான்.உயிரினங்களின் வாழ்வியல் சூழ்நிலையையும், போராட்டத்தையும் அழகாக படமாக்கியுள்ளார்.

 

இமயமலையை சுற்றிப் பார்த்தது போன்ற ஒரு பிரமையை இக்காணொளி தருகிறது.பனி உருகி குகை பாதைகளை ஏற்படுத்தி ஆறுகளாக பாய்வது அருமை. அங்கும் சில இடங்களில் அலைமோதும் பக்த கோடிகள் கூட்டம். விலங்குகளுக்குள்ளும்  உள்ள‌ அன்பு ,ஒற்றுமை உணர்வு, பகிர்ந்துண்ணுதல் போன்றவற்றையும் காணொளி ஆவணப் படுத்துகின்றது. இது கண்டு க‌ளிக்க வேண்டிய காணொளி.

இயற்கையை இரசிக்காதவர்களால் அதனை அறியவோ உணரவோ முடியாது!!!!!!

இதுவும் இந்தியாதான்! நமக்கு தெரிவது நல்ல விடயங்கள் சிலருக்கு தெரிவதெல்லாம் விவகாரமான் விடயங்களே!!!!

இயற்கையை நேசிப்போம்!!!!

இயற்கை சூழலை பாதுகாப்போம்!!!!

கண்டு களியுங்கள்!!!

நன்றி

சாதி வாரிக் கணக்கெடுப்பில் மனிதர்கள் சாதி மறுப்போம்!

கிடப்பதெல்லாம் கிடக்கட்டும் கிழவனைத் தூக்கி மனையில் வைத்த கதையாய் ஏப்ரல் 23ஆம் தேதியில் இருந்து சாதி வாரிக் கண்க்கெடுப்பு எடுக்கப் போகிறார்களாம்.இது எந்த விதத்திலாவது உதவியாக் இருக்கும் என நமக்குத் தோண்ற‌வில்லை.

இட ஒதுக்கீடு சாதிரீதியாக் பிரித்து அளித்தால் அனைவரும் முன்னேறுவார் என்ற கருத்து உண்டு என்றாலும் இட ஒதுக்கீடு என்பது மட்டும் அனைத்தையும் தீர்க்கக் கூடிய சர்வ ரோஹனி அல்ல என்பதும்,அதனை மட்டும் வைத்து ஒன்றும் செய்ய முடியாது என்பது நம் கருத்து.என்ன ஒவ்வொரு சாதியிலும் ஒரு உயர் வகுப்பினர் உருவாகி அவர்களுடைய சந்ததியினர் மட்டும்  இட ஒதுக்கீட்டின் பலனை அறுவடை செய்வார்கள்.

கல்வி சுகாதாரம் இரண்டும் இலவசம் ஆக்கப்பட்வேண்டும்.ஒரு மாவட்டத்தில் வாழ்பவர்கள் அவர்களுக்குறிய அனைத்து வாழ்வாதாரங்கள்,அரசு சம்பந்தப்பட்ட வேலைகள் அனைத்தையும் அதிக பட்சம் மாவட்டத் தலை நக்ர் அள்விலேயே முடிக்கும் அளவு செய்தால் பெரு நகரங்களை நோக்கிய மக்களின் இடப்பெயர்வு தடுக்கப்படும்.அரசின் மக்கள் நலப் பணிகள் வெளிப்படையாக கண்காணிக்கும் படி இருந்தால் ஊழலும் குறையும்.ஒருவர்   ச்ட்டமன்ற உறுப்பினர் அல்லது பாரளுமன்ற உறுப்பினராக் குறிப்பிட்ட காலம் மட்டுமே பணியாற்ற‌லாம் என மாற்ரம் ஏற்படுவது பல் புதிய தலைவர்கள் தோன்ற‌ வழி வகுக்கும்.வாரிசு அரசியலை ஒரு அள்வுக்கு தடுக்கும். கொண்டுவருவது

இதையெல்லாம் விட்டு விட்டு சாதி வாரிக் கண்க்கெடுப்பு என்பது எதில் போய் முடியும்?

'அ 'சாதி 15% இருக்கிறார்கள் என வைத்துக் கொள்வோம்.அப்போது அவர்களின் தலைவனாக பல சாதித்தலைவர்கள் முயற்சி செய்து சாதி உணர்வைத் தூண்டுவார். உடனே 'அ' அல்லாத‌வர்கள் அதற்கு எதிராக திரும்புவர்.இம்மாதிரி கண்க்கெடுப்பு ஏற்கென‌வெ ஒரு அள்விற்கு அரசு கணித்தே வைத்து இருக்கும்.அதனால்தான் சரியாக ஒரு தொகுதியில் பெரும்பான்மை இன வேட்பாள்ரையே அனைத்து கட்சிகளும் நிறுத்தும். இபோதைய இட ஒதுக்கீடு கூட ஆங்கிலேயர் ஆட்சிக் கால்த்தில் எடுக்கப்பட்ட ஒரு கண்க்கீட்டின் அள்விலேயே வழங்கப் படுகிறது.

இடஒதுக்கீட்டுக்கு எதிராக பேசுகிறேன் என கருத்து திரிபு செய்ய வேண்டாம்.பல சமூக ஒடுக்குதலினால் ஒடுக்கப்ப்ட்ட மக்களுக்கு இட ஒதுக்கீடு இபோது நடைமுறையில் உள்ளது.அதனை நாம் கொஞ்சம் கொஞ்சமாக் அது தேவையில்லை என்னும் நிலையை நோக்கி செல்ல முடியுமா என பாருங்கள் என்றே கூறுகிறோம்.

இப்போது இந்த கண்க்கீடு மூலம் இட ஒதுக்கீடு விகிதங்கள் மாற்றப் பட்டால் சமூக முரண்கள் அதிகம எழலாம்.இந்த கண்க்கீடுகள் இந்த அள்வில் நிற்காது.

உலகின் பல நாடுகளில் இப்படி கணக்கீடுகள் எடுத்து அடையாள அட்டையிலேயே மதம்,இனம்,மொழி  குறிக்கப்பட்டதுதான் பல பிரச்சினைகளுக்கு காரணம்.

வாழும் இடம்,சூழல் சார்ந்த சொந்தக் காலில் நிற்கக் கூடிய  எளிய இலவச கல்விமுறை ,அனைவருக்குமே  வேலை வாய்ப்பு வழங்க இயலாத  அரசுகள் இப்படி மக்களை பிரித்து மோதவிட்டு வேடிக்கை பார்ப்பது வரலாற்றில் சாதாரணமான ஒன்று என்றாலும் இது தேவையற்ற‌ தவிர்க்க கூடிய ஒரு விடயம்.

மனிதர்கள் கண்க்கெடுப்பின் போது "சாதி இல்லை என்ற 4 ஆம் பிரிவை" தேர்வு செய்ய வேண்டுகிறோம். சாதி மறுப்பு மனிதர்களின் எண்ணிக்கைதான்   தமிழ்நாட்டின் மக்கள் தொகை என நாம் ஏற்கிறோம்.

நன்றி

சுனாமி செயல்பாடுகள் பாதுகாப்பு பற்றி அறிவோம்:காணொளி

வணக்கம் நண்பர்களே

சுனாமி வரவில்லை என் அனைவரும் நிம்மதி பெருமூச்சு விடும் வேளையில் இது பற்றி கொஞ்சம் விடயம் அறிவதும் இன்றியமையாதது.

சுனாமி என்னும் ஜப்பானிய மொழி வார்த்தையை ஆழிப் பேர‌லை அல்லது கடற்கோள் என மொழியாக்கம் செய்ய்லாம். இக்காணொளி சுனாமி ஏன் நடக்கிறது ? அதற்கான் பாதுகாப்பு ஏற்பாடுகள் பற்றி விளக்குகிறது.

பூமியின் அடுக்குகளான டாக்டோனிக் தக்டுகள் ஒன்றின் மீது ஒன்று மோதி த்ள்ளுவதுதான பூகம்பம்.சுனாமி இரண்டின் காரணமாக இக்காணொளியில் கூறுகின்றனர். சுனாமி என்பது க்டலுக்கு அடியில் ஏற்படுவெதே வித்தியாசம்.இது 25,000 மடங்கு ஹிரோசிமா அணு குண்டை விட சக்தி வாய்ந்தது என்வும் கூறுகின்றனர்.

பசிஃபிக் கடலில் பல முன் அறியும் கருவிகளை அமரிக்க அரசு பொருத்தி உள்ளதும் இது கண்காணிக்கப்பட்டு சாட்டிலைட் மூலம் எளிதில் த்கவல்கள் பெற்பட்டு அறிவிக்கப்படுகின்றன.

இந்திய பெருங்கடலில் இப்படி அமைப்பு இல்லை என்பது மிக வருத்ததிற்கு உரிய விடயம்.

இயற்கை சீற்றம் என்பதை தவிர்க்க இயலாது என்பதை உணர்ந்து அதில் இருந்து மக்களை காப்பதே முக்கிய நோக்கமாக் நாடுகள் நினைக்கவேண்டும்.சுனாமி பாதிப்பை குறைக்க நாடுகளுக்கிடையே ஒத்துழைப்பு,த்கவல் பரிமாற்றம் மிக அவசியம்.

சுற்றுச் சூழல் பாதுகாப்பு என்பது மிக முக்கியமான் ஒன்று என்பதை அனைவரும் உணர்ந்து தகுந்த எதிர் நடவடிக்கை எடுத்து பாதுகாப்பாக இருக்க வேண்டும்.

பாருங்கள் காணொளியை இன்னும் பல் விவரங்கள் அறீவீர்கள்!

நன்றி
ஆவணப்படம்

சுனாமி பற்றி தகவல்கள்

பெருவெடிப்பு [Big Bang] மத புத்தகத்தில் குறிப்பிடப்பட்டு உள்ளதா ?; ஆய்வுக் காணொளி!

வணக்கம் நண்பர்களே!

மதபுத்தகங்களில் அறிவியல் என்பது ஒரு மதப்பிரசார உத்தி என்பதை மதபிரச்சாரகர்கள் தவிர அனைவரும் அறிந்து இருந்தாலும் அவ்ர்கள் மனம் தளராது விள்க்குகின்றார்.

இணையத்தில் இமாதிரி பிரச்சார உத்திகளை ஆராய்ந்து உண்மையை என்ன்,எப்படி என விள்க்கும் பல காணொளிகள் உண்டு.ஆகவே ஒவொவொரு மத அறிவியல் பிரசாரத்திற்கும் எதிரான காணொளி வழங்குவோம் என்பதை மகிழ்ச்சியோடு தெரிவிக்கிறோம்.

இதற்கு விள்க்கம் அவசியமில்லை ஏன் எனில் திறமையான மொழி பெயர்ப்பு+அடைப்புக்குறியினுள் சொற்கள் போட்டு எந்த பொருள் வேண்டுமானாலும் கொண்டுவரமுடியும் என்பதை அறிந்தால் இது ஒன்றும் பெரிய வித்தையில்லை என்பதை அறிவீர்கள்.

"ஒவ்வொரு [மத அறிவியல்] பிரச்சாரத்திற்கும் எதிர் பிரசாரம் உண்டு"

மத அறிவியல் என்னும் பிரசாரத்தை எப்படி சமாளிப்பது என்ற நம் முந்தைய பதிவு!.

http://saarvaakan.blogspot.com/2011/03/blog-post_29.html

நாம் என்ன சொல்ல வருகிறோம்?

மதவாதிகள்[அனைவருக்கும் பொருந்தும் மத சார்பற்ற‌] அறவியல் பேசினால் நம்மிடம் எதிர்ப்பில்லை. மதத்தில் அறிவியல் என்ற போர்வையில் அறம் அல்லாத  இயல்களை[சட்டங்கள்] நியாயப்படுத்துவதால் அதை எதிர்க்க வேண்டிய கட்டாயத்துக்கு உள்ளகிறோம்.

காணொளி கண்டு இரசியுங்கள்!!!!! 

ஆகவே பரிணாம எதிர்ப்புக் கொள்கையோடு, மத அறிவியலையும் சேர்த்து அன்போடு கவனிப்போம்!!!!!!!! 

நன்றி

இது நம் கம்பெனி விளமபரம்,இங்கே ஒரிஜினல் மத பிரசார காணொளிகளும் அதற்கு எதிர் பிரச்சார காணொளிகளும் சிற‌ந்த தரத்தில்,காப்பிரைட்டுடன் கிடைக்கும்.ஸ்பெசல் ஆர்டரின் பேரில் [அறிவார்ந்த]வடிவமைத்தும் தரப்படும்.

அப்புறம் நாம் மத சார்பற்றவர் என்று நிரூபிக்க அகில உலக் பெரும் பிரசாரகர் ஹாருண் யாஹ்ய[Harum yahya] அவர்களின் காணொளியும் அளிக்கிறோம்.

ஆகவே யார் யாருக்கு எந்த காணொளி பிடிக்குமோ சண்டை போடாமல் பார்த்து இரசிக்க வேண்டுகிறேன்.

ஹாரூண் யாஹ்யாவின் பிரச்சார உத்திகளை மட்டும் எடுத்து பயன்படுத்தி அவரின் பெயரை குறிப்பிடாமல் இருக்கும் போட்டி பிரச்சாரகர்களுக்கு கடும் கண்டனம்.!!!!!!!

அன்னைத் தமிழில் அழகாக மத அறிவியல் வழங்கும் ஒரிஜினல் ஹாருண் யாஹ்யாவின் மத அறிவியல் பிரசாரத்தை மட்டும் கேளுங்கள்.போலிகளை கண்டு ஏமாறாதீர்!!!!!!

நமது விள்ம்பரதாரர்!!!!!!!!!!!!!!!!!!!!!

டெய்லர் தொடர் வரிசையின் நிரூபணம்

டெய்லர்  தொடர் வரிசையின் நிரூபணம்

வணக்கம் நண்பர்களே!

டெயலர் தொடர் வரிசை என்பது குறித்து உங்களில் பெரும்பானமையோர் அறிந்து இருக்கலாம.இத்தொடரில் அதற்கு நிரூபணம் தருவது எப்படி என்பதை எளிதாக கற்போம்.

சரி தொடர்வரிசை என்றால் என்ன?

ஒரு குறிபிட்ட எண்களோ , மாறிகளின் தொடர்போ[function of variables] ஒரு குறிப்பிட்ட சார்பு வீதத்தில் முன் செல்வது என கூறலாம், இப்பப்டிப்பட்ட கூட்டுத் தொடருக்கு பல சம்யங்களில்நிலையான எண்[finite number] அல்லது நிலையான மாறித் தொடர்பு[finite function] விடை உண்டு.

ஏன் பல சமயங்களில் என்று கூறுகிறோம்? சில சமயம் விடை முடிவிலி கிடைக்கலாம் என்பதற்காக அப்படி கூறினோம்.அப்போது முடிவிலி நிலையான எண் இல்லையா எனில் ,இதனை இல்லை என்று ஏற்கெனவே இப்பதிவில் கூறியுள்ளோம். நண்பர்கள் எப்போதும் ஒரு விடயத்தை மனதில் இருத்த வேண்டும்,ஒவ்வோரு விதிக்கும் எல்லைகள் உண்டு,எல்லைகளில் விதியை பொருத்துவதற்கு சில  மாறுதல்களை செய்ய வேண்டும்.

ஆகவெ முதலில் கற்கும் நண்பர்கள் எளிய வழியில் எந்த வித ஐயத்திற்கும் இடமில்லாத‌ விதி பொருந்தும் இடைவெளிகளில் நன்கு கற்று ஆராய்ந்து பிறகு விதியை சிறிது மாறுதலுடன் பயன்படுத்த வேண்டிய எல்லைகளுக்கு செல்வது நல்லது.  

இதன் எதிர் வினையும் உண்மையே ஒரு மாறித் தொடர்பு ,அல்லது நிலை எண்ணை முடிவிலி[அல்லது முடிவுறும்] கூட்டுத் தொடராக வரையறுக்க முடியும்.

எ.கா  

a)1,+2+,+3+4+5+,...+.n=n(n+1)/2

 b)

ஆகவே எளிதாக கூறினால் (பல) முடிவிலி தொடருக்கு சமமான நிலை எண் அல்லது ஒரு நிலையான் மாறித் தொடர்பு[function of variables] காண முடியும்.

இத எதிர்வினையும் உண்மையே

“பல‌ நிலையான‌ மாறித் தொடர்புகளை [finite functions] முடிவிலி தொடராக எழுத முடியும்”.

“A finite function can be expressed in terms of an infinite sum “

“Finite function=continuously differentiable”

நிலையான் மாறித் தொடர்பு எனில் தொடர்ச்சியாக சிறுமாற்ற விகிதம் கண்டறியத் தக்கது என பொருள் கொள்கிறோம்.

இப்பதிவில் எதிர்வினையை பற்றி மட்டுமே பார்க்கப்போகிறோம்.அப்போது முடிவிலி தொடர்களின் கூடுதலை நிலை எண் அல்லது மாறித் தொடர்பாக மாற்றுவது குறித்து கற்போம் என்கிறீர்களா. அதுவும் பிறகு முயற்சி செய்வோம்!

                                             

இப்போது எதிர்வினையான  ஒரு மாறித் தொடர்பை முடிவிலி தொடர்பாக எழுதுவதை கற்போம்.

என்ன கொஞ்சம் சிக்கலாக் இருப்பது போல் உள்ளதா!.சரி மிக மிக எளிமையாக் பேசுவோம்.

"ஒரு எதிர்கால சூழல் ஆனது கடந்தகால் நிகழ்கால சூழலை பொறுத்து இருக்கிறது"

இது என்ன மகா பெரிய தத்துவம்? இதுதான் அனைவருக்குமே தெரியுமே என்றால் அப்பாடா உங்களுக்கு புரியும் வகையில் பேசுவது நம்க்கு மகிழ்வே!.நாம் எழுதுவது உங்களுக்கு புரியவில்லை,அல்லது பிடிக்கவில்லை எனில் எழுதாமல் இருப்பதே நலம் என நினைக்கிறேன்.

ஆகவே புரியும் வகையில் மட்டுமே எளிமையாக் எப்போதும் எழுதுவோம் எனவே கூறுகிறோம்.

ஒரு இடத்தில் ஒரு மாறக்கூடிய  சூழலில் இருக்கிறோம்.அதில் இருந்து அருகே உள்ள இன்னொரு இடத்திற்கு செல்ல வேண்டும்.நாம் உள்ள இடத்தில் அறிந்த விவரங்களைக் கொண்டு அருகே உள்ள இடத்தின் சூழலை  அறிய முயல்வதுதான் இந்த தொடர்வரிசை கணித்தல் [prediction or extrapolation] என கூறலாம்.

இபோது நாம் இருக்கும் இடம் 3, இத்ற்கு முன் 2,அதற்கு முன்1 எனில் இத்தொடர் வரிசை எப்படி இருக்கும்?

1,2,3,4,5,6,7 என்று இருக்க வேண்டும்.இது சரிதான் என்றாலும் எப்போதும் சரியாக இருக்க வேண்டிய அவசியம் இல்லை.மொத்தம் மூன்று அள்வுகளை வைத்து இன்னும் மூன்று அள்வுகளை கணிப்பது என்பது பல நிகழ்வுகளில் சரியாக இருக்காது.அது பற்றி பிறகு பார்ப்போம்.

டெய்லர் தொடர் என்பது ஒரு  (முதல்) புள்ளியின் சூழல் குறித்த அளவைகள் கொண்டு  அறிந்து அருகே உள்ள  இன்னொரு (இரண்டாம்) புள்ளியின் சூழலை அள்ப்பது என கொள்ளலாம்.

f(x+a)=

 

If a=0

 

x=இப்போதைய (முதல்) புள்ளி

f(x)= (முதல்) புள்ளியின் சூழலின் அளவு

a=அருகாமை தூரம்

x+a= அருகாமை (இரண்டாம்)   புள்ளி

f(x+a)= அருகாமை  ((இரண்டாம்)  புள்ளியின் சூழலின் அளவு

f’(x)= முதல் சிறுமாற்ற விகிதம்[first derivative]

f²(x)= இரண்டாவது சிறுமாற்ற விகிதம்

..

.

.

f^N(x)= N வது சிறுமாற்ற விகிதம்

N=1,2,3,…ω

ஆகவே டெய்லர் தொடர்வரிசை என்பது முதல் புள்ளியின் அள்வு,சூழ,சூழலின் மாற்றங்களின் அடுக்குகளின் அள்வுகள் மூலம் அடுத்த புள்ளியின் சூழலின் அளவை கணிக்கிறோம்.

"ஆகவே எந்த ஒரு சிக்க்லான மாறித் தொடர்பையும் முடிவிலி எளிய மாறித் தொடர் அமைப்புகளாக் பிரிக்க இயலும்"

“Any function of higher order complexity can be expressed as a summation of simple power series”.

எங்கிருந்து எங்கே வருகிறோம் என புரிகிறதா?

சிறுமாற்ற விகிதம்[derivative] கண்டு பிடிக்கத் தெரிந்தால் கண்டறிந்து மதிப்புகளை பிரதியிட்டால் டெய்லர் தொடர் தேர்வு ரீதியாக முடிந்தது.ஆனால் அது என்ன என்பதையே அவதானிக்கிறோம்.

இப்போது நிரூபணத்திற்கு செல்வோம்

டெய்லர் தொடர்வரிசை அடுக்குத் தொடர் வரிசையின் ஒரு வகை ஆகும். அடுக்குத் தொடர் வரிசையின் குணகங்களை(coefficients) கண்டறிந்தால் டெய்லர் தொடர்வரிசை தயார் ஆகிவிடும்.

அடுக்குத் தொடர் வரிசை என்றால் என்ன எந்த ஒரு சிக்கலான மாறித் தொடர்பையும் முடிவிலி எளிய மாறி அடுக்குகளின் கூட்டுத் தொடர் வரிசையாக் கூற முடியும்.

a0,a1,a2,… கண்டறிந்தால் டெயலர் தொடருக்கு நிரூபணம் ஆகிவிடும்.

இப்போது x=c என பிரதியிடுவோம்.

f(c)=a₀

இபோது முதல் சிறுமாற்ற விகிதம் கண்டு பிடித்து மீண்டும் x=c என பிரதியிட்டால் a₁ ன் மதிப்பு கிடைக்கும்

f^’(x)=0+a₁+2*a_2*(x-c)+3a₃(x-c)²+….+n.a_n.(x-c)(^n-1)+….

இப்போது x=c என பிரதியிடுவோம்.

f¹[c]=a₁

…..

f ²[c]/(2!)=a2

….

…

f ⁿ[c]/(n!)=a_n

இந்த மதிப்புகளை அடுக்குத் தொடர் வரிசையில் பிரதியிட்டால் டெய்லர் தொடர் கிடைக்கும்.

f(x+a)=

 

If a=0 என பிரதியிட்டால் மெக்லாரின் தொடர்வரிசை கிடைக்கும்.

 

ஆகவே டெய்லர் தொடர்வரிசை நிரூபிக்கப்பட்டது.

இப்போது விதண்டாவாதம்

சரி அடுக்குத் தொடர் வரிசையில் இருந்து டெயலர்,மெக்லாரின் தொடர்வரிசை கண்டு பிடித்தோம் இதை எப்படி நிரூபணமாக் எடுக்க முடியும்?. இது அடுக்குத் தொடர்வரிசை எந்த அளவு உண்மையோ ,டெய்லர் தொடர்வரிசையும் அந்த அளவே உண்மையாக் இருக்க முடியும்???????????.

சரியான் கருத்து எனினும் அடுக்குத் தொடருக்கு இன்னொரு அடிப்படை இப்படியே ஒன்று[1] என்ற எண்ணின் வரையறை வரை செல்லும்.அடுக்குத் தொடரின் நிரூபண்ம் கொஞ்சம் கடினம்!!!!!!!!!!!!!.

கடினம் என்ற சொல்லை அதற்கு இன்னும் பல் அடிப்படைத் தேற்றங்கள் தேவைப்படும் என்ற பொருளிலேயே கூறுகிறோம்.தொடர்சியான் எளிய அமைப்புகளின் கூட்டமைப்பு சிக்க்லான அமைப்பை உருவாக்கும் என்பதையும் அடுக்குத் தொடர் வர்சையில் இருந்து அறியலாம்.

இங்கே அறிய விரும்புபவர்கள் அறியலாம்.

http://www.proofwiki.org/wiki/Derivative_of_Complex_Power_Series/Proof_1

ஆகவே முதலில் அடுக்குத் தொடர்வரிசை நிரூபண்ம்  எங்களுக்கு புரியும் வரை டெய்லர் நிரூபண்மும் செல்லாது செல்லாது!,என எதிர் பதிவு இட விரும்பும் நண்பர்கள் இட வலியுறுத்துகிறோம்.

கணிதத்தில் மட்டுமே மிக சரியான நிரூபணம் தர முடியும் என்றாலும் அது சாமான்யனுக்கும் புரியும் வரையில் எளிமைப்படுத்துவது என்பதற்கு கடும் ,தொடர் உழைப்பு தேவைப்படும்.அதில் நாம் ஒரு துரும்பை எடுத்து விளக்க  முயற்சிக்கிறோம் அவ்வளவுதான்!.

எல்லாவற்றுக்கும் அடிப்படை ஒன்றே,அந்த அடிப்படையில் இருந்தே அனைத்து அறிவியலும் கிளைத்து தழைத்தன என்பதை அறியாமல், எதையும்  பிற விளக்கங்கள் சாராமல் அறிய இயலாது என்பதை அறியாமல்  எழும் கேள்விகளை புறக்கணிப்போம்.கற்றல் என்னும் தொடர் தேடலை தொடர்வோம்.

இப்பதிவின் சாரம்

1.ஒரு (நிலையான) கடின்மான (சிக்க்லான) மாறித் தொடர்புக்கு சமமான  எளிமையான் மாறி அடுக்கு தொடர்வரிசை உண்டு. 

2.அடுக்குத் தொடர்வரிசை என்பதை இரு வகைகள்தான் டெய்லர்,மெக்லாரின் தொடர் வரிசைகள்.அடுக்குத் தொடர்வரிசையில் சில கணித செயல்க‌ள் + பிரதியிடுதல் மூலம் டெய்லர்,மெக்லாரின் தொடர் வருவிக்க முடியும்.

3.இவை மாறித் தொடர்பு எளிமைப்படுத்தல்[function approximation],எதிர்(கடந்த)கால நிகழ்வு கணித்தல்[prediction or extrapolation] போன்ற விடய‌ங்களுக்கு பயன்படுகின்றன.