இரமானுஜம் முழு எண்கள் கொள்கையியல்,(number theroy) வடிவ கணிதம்(geometry),அல்ஜீப்ரா(algebra) ப்ன்ற பல கணித முறைகளில் மேதமை பெற்றிருந்தார்.வடிவ கணிதத்திற்கு எடுத்துக்காட்டாக இப்பதிவில் அவர் தீர்வு கண்ட ஒரு கணிதப் புதிரை பார்க்கலாம்.
அவர் தீர்வு காண எடுத்துக் கொண்ட புதிர் இப்படி கூறலாம்.
ஒரு வட்டத்தின் பரப்பிற்கு சமமான பரப்பு கொண்ட சதுரத்தை வடிவ கணிதம் மூலம அமைக்க முடியுமா?(squaring the circle)
(அளவு கோள்(ruler) ,காம்பஸ் மட்டுமே ப்யன் படுத்த வேண்டும்)
இது மிகவும் பழமையான் புதிர்.பொ.மு(BC) 1800 ல் எகிப்தியர்கள் முயற்சி செய்தனர் என்றால் மிக ஆச்சர்யமாக் இருக்கும்.П(pi) என்பதின் மதிப்பு இதுதான் என்று வரையறுக்க்படாததால் இது தீர்வு காண முடியாத புதிர் என்று 1882 CE ல் நிரூபிக்கப் பட்டது.
இருந்தாலும் தோராய தீர்வுகள் π (pi) ன் மதிப்பை வைத்து இப்புதிருக்கு தீர்வு கண்டனர்.அதில் நமது இரமானுஜமும் ஒருவர்.
அவர் ஒரு(1) அலகு ஆரம் உள்ள வட்டத்தின் பரப்பை தீர்வுக்கு எடுத்துக் கொண்டார்.இவ்வட்டத்தின் பரப்பு=π (pi) அலகு^2.
சதுரத்தின் பக்கம் என்பது π ன் வர்க்க மூலமாக் இருக்கும்.
இதற்கு Dan W. Gaddy என்பவரின் எளிய தீர்வை முதலில் பார்க்கலாம்.
π=
(root of 2)+
( root of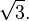 3)=1.414+1.716=3.130( approximate)
இத்னை வடிவ கணிதத்தில் எப்படி வடிவமைப்பது என்று காணொளியில் காட்டப் பட்டு உள்ளது.
(root of 2)+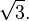( root of 3)=1.414+1.716=3.130( approximate)இத்னை வடிவ கணிதத்தில் எப்படி வடிவமைப்பது என்று காணொளியில் காட்டப் பட்டு உள்ளது.
இப்போது நம் இரமானுஜம் ஃபார்முலா தருகிறார்
![\left(9^2 + \frac{19^2}{22}\right)^{1/4} = \sqrt[4]{\frac{2143}{22}} = 3.1415926525826461252\dots](http://upload.wikimedia.org/math/b/a/f/baf1a09003c20516c6db779602fe9b94.png)
.அதனை வடிவ கணிதத்திலும் அமைக்கிறார்.கிடைப்பது 8 தசம் தானங்கள் துல்லியமான் விடை.எப்படி என்று கொஞ்சம் யோசியுங்கள்.
O என்பது வட்டத்தின் மையம் . PR என்பது விட்டம் RT .என்பது விட்டத்தில் 1/6 (ஆறில் ஒரு பங்கு).,TQ=RS.
மீதம் உள்ளதை அளந்து பார்த்தால் விடை காண முடியும்.முயற்சியுங்கள்.
RC என்பது சதுரத்தின் பக்க அளவான square root of π (pi)
இரமனுஜத்தின் தீர்வு அடுத்த பதிவில்.!!!!!!!!!!!
http://www.song-of-songs.net/Squaring_the_Circle.html
மீதம் உள்ளதை அளந்து பார்த்தால் விடை காண முடியும்.முயற்சியுங்கள்.
RC என்பது சதுரத்தின் பக்க அளவான square root of π (pi)
இரமனுஜத்தின் தீர்வு அடுத்த பதிவில்.!!!!!!!!!!!
http://www.song-of-songs.net/Squaring_the_Circle.html
நண்பரே.
ReplyDeleteஇராமானுஜ பார்மலாவும், image ம் பதிவில் சரியாக தெரியவில்லை.
என் மூளைக்கு எட்டியவரை, ஒரு கயிற்றை எடுத்து அதை வட்டவடிவமாக்கி, அதை மறுப்படியும் சதுரமாக்கினால், வட்டத்தின் பரப்பு அளவு கொண்ட சதுர பரப்பு வந்து விடுமா??.
நண்பர்களே!
ReplyDeleteகூடுமானவரை இரமனுஜத்தின் பல கணிதமுறைகளையும் எளிமைப் படுத்தி தர முயற்சிக்கிறேன்.இது குறித்த ஆலோசனைகள்,திருத்தங்கள் வரவேற்கப் படுகின்றன.
நன்றி
நன்றி நரேன்,
ReplyDeleteசரி செய்தாயிற்று
/என் மூளைக்கு எட்டியவரை, ஒரு கயிற்றை எடுத்து அதை வட்டவடிவமாக்கி, அதை மறுப்படியும் சதுரமாக்கினால், வட்டத்தின் பரப்பு அளவு கொண்ட சதுர பரப்பு வந்து விடுமா??/
ReplyDeleteவராது நரேன்.வட்டத்தின் சுற்றளவுதான் கயிறின் நீளம்.அப்போது வட்டத்தின் சுற்றளவில் நாலில் ஒரு பங்கு சதுரத்தின் பக்கத்தின் அளவு.
r=radius(ஆரம்)
வட்டத்தின் சுற்றளவு=2π r
சதுரத்தின் பக்கத்தின் அளவு=2π r/4=π r/2
வட்ட்த்தின் பரப்பளவு=π r^2
சதுரத்தின் பரப்பளவு (π^2* r^2)/4